10. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD\perp AB$于点$D$. 若$AC = 2$,$BC = 1$,则$\sin\angle ACD$的值为 ( )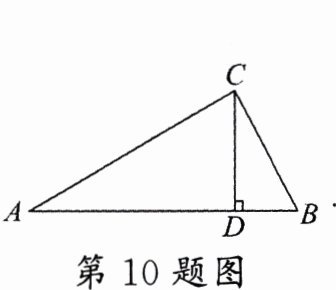
A. $\frac{\sqrt{5}}{3}$
B. $\frac{2\sqrt{5}}{5}$
C. $\frac{\sqrt{5}}{2}$
D. $\frac{2}{3}$

A. $\frac{\sqrt{5}}{3}$
B. $\frac{2\sqrt{5}}{5}$
C. $\frac{\sqrt{5}}{2}$
D. $\frac{2}{3}$
答案:
B
11. (2024·南阳模拟) 如图,$AB$为$\odot O$的直径,$C$,$D$为$\odot O$上两点,连接$AC$,$CD$和$BD$,若$AC = 4$,$\odot O$的半径为$3$,则$\tan D$的值为( )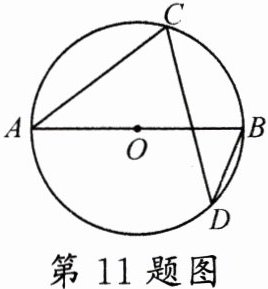
A. $\frac{2}{3}$
B. $\frac{2\sqrt{5}}{5}$
C. $\frac{3}{2}$
D. $\frac{\sqrt{5}}{2}$

A. $\frac{2}{3}$
B. $\frac{2\sqrt{5}}{5}$
C. $\frac{3}{2}$
D. $\frac{\sqrt{5}}{2}$
答案:
D
12. 如图,在$\triangle ABC$中,$AB = AC = 5$,$BC = 8$. 若$\angle BPC = \frac{1}{2}\angle BAC$,则$\cos\angle BPC =$______. 

答案:
$\frac{3}{5}$
13. 如图,圆$O$的直径$AB = 8$,$AC = 3CB$,过$C$作$AB$的垂线交圆$O$于$M$,$N$两点,连接$MB$,则$\angle MBA$的余弦值为______. 

答案:
$\frac{1}{2}$
14. 如图,在$\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AB = AC$,点$D$为边$AC$的中点,$DE\perp BC$于点$E$,连接$BD$,则$\tan\angle DBC =$______. 

答案:
$\frac{1}{3}$
15. 如图,若想求$\tan15^{\circ}$的值,可先画$Rt\triangle ABC$. 使$\angle C = 90^{\circ}$,$\angle BAC = 30^{\circ}$,再延长$CA$到$D$,使$DA = AB$,连接$BD$. 你能求出$\tan15^{\circ}$的值吗?请你试一试. 

答案:
因为$AD = AB$,所以$\angle D=\angle ABD$,又因为$\angle D+\angle ABD = 30^{\circ}$,所以$\angle D = 15^{\circ}$。在$Rt\triangle ABC$中,$\angle BAC = 30^{\circ}$,设$BC = k(k>0)$,则$AB = 2k$,$AC=\sqrt{3}k$,所以$AD = 2k$,所以$\tan D=\frac{BC}{DC}=\frac{BC}{AD + AC}=\frac{k}{(2+\sqrt{3})k}=2 - \sqrt{3}$,即$\tan15^{\circ}=2-\sqrt{3}$
16. 如图,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 8$,$BC = 6$,将其如图折叠使点$A$与点$B$重合,折痕为$DE$,连接$BE$,则$\tan\angle CBE$的值为 ( )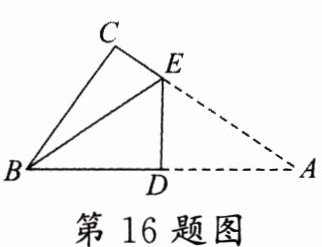
A. $\frac{24}{7}$
B. $\frac{\sqrt{7}}{3}$
C. $\frac{7}{24}$
D. $\frac{1}{3}$

A. $\frac{24}{7}$
B. $\frac{\sqrt{7}}{3}$
C. $\frac{7}{24}$
D. $\frac{1}{3}$
答案:
C
17. 如图,折叠矩形$ABCD$的一边$AD$,使点$D$落在$BC$边的点$F$处,已知$AB = 8\ cm$,$BC = 10\ cm$,则$\tan\angle EAF$的值为______. 

答案:
$\frac{1}{2}$
查看更多完整答案,请扫码查看


