1. 在$\triangle ABC$和$\triangle A'B'C'$中,$\angle A = 68^{\circ}$,$\angle B = 40^{\circ}$,$\angle A' = 68^{\circ}$,$\angle C' = 72^{\circ}$,则这两个三角形( )
A. 全等
B. 相似
C. 不相似
D. 无法确定
A. 全等
B. 相似
C. 不相似
D. 无法确定
答案:
B
2. 下列各组图形中有可能不相似的是( )
A. 各有一个角是45°的两个等腰三角形
B. 各有一个角是60°的两个等腰三角形
C. 各有一个角是105°的两个等腰三角形
D. 两个等腰直角三角形
A. 各有一个角是45°的两个等腰三角形
B. 各有一个角是60°的两个等腰三角形
C. 各有一个角是105°的两个等腰三角形
D. 两个等腰直角三角形
答案:
A
3. 如图,已知$\triangle ABC$和$\triangle ABD$都是$\odot O$的内接三角形,$AC$和$BD$相交于点$E$,则与$\triangle ADE$相似的三角形是( )
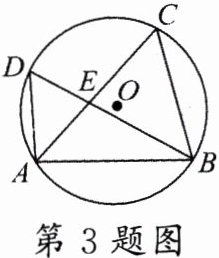
A. $\triangle BCE$
B. $\triangle ABC$
C. $\triangle ABD$
D. $\triangle ABE$

A. $\triangle BCE$
B. $\triangle ABC$
C. $\triangle ABD$
D. $\triangle ABE$
答案:
A
4.(2024·青海)如图,$AC$和$BD$相交于点$O$,请你添加一个条件________________,使得$\triangle AOB\backsim\triangle COD$.


答案:
$\angle A=\angle C$(答案不唯一)
5.(2024·周口郸城县期中)如图,在平行四边形$ABCD$中,点$E$为$BC$边上一点,连接$DE$,点$F$为线段$DE$上一点,且$\angle AFE = \angle B$. 求证:$\triangle ADF\backsim\triangle DEC$.
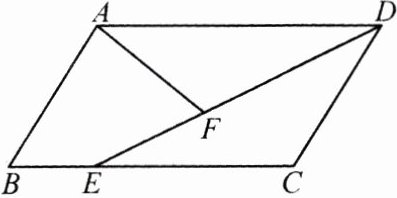

答案:
证明:$\because$四边形$ABCD$是平行四边形,$\therefore AB// CD$,$AD// BC$,$\therefore\angle C+\angle B = 180^{\circ}$,$\angle ADF=\angle DEC$,$\because\angle AFD+\angle AFE = 180^{\circ}$,$\angle AFE=\angle B$,$\therefore\angle AFD=\angle C$,$\therefore\triangle ADF\sim\triangle DEC$
6.(教材P36练习2变式)如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD\perp AB$于点$D$,则图中相似三角形共有( )

A. 1对
B. 2对
C. 3对
D. 4对

A. 1对
B. 2对
C. 3对
D. 4对
答案:
C
7. 在$Rt\triangle ABC$和$Rt\triangle A'B'C'$中,$\angle C = \angle C' = 90^{\circ}$,若添加一个条件,使得$Rt\triangle ABC\backsim Rt\triangle A'B'C'$,则下列条件中不符合要求的是( )
A. $\angle A = \angle A'$
B. $\angle B = \angle B'$
C. $\frac{AB}{A'B'}=\frac{AC}{A'C'}$
D. $\frac{AB}{A'C'}=\frac{AC}{B'C'}$
A. $\angle A = \angle A'$
B. $\angle B = \angle B'$
C. $\frac{AB}{A'B'}=\frac{AC}{A'C'}$
D. $\frac{AB}{A'C'}=\frac{AC}{B'C'}$
答案:
D
8. 如图,$\angle ABD = \angle BDC = 90^{\circ}$,$\angle A = \angle CBD$,$AB = 3$,$BD = 2$,则$CD$的长为( )

A. $\frac{3}{4}$
B. $\frac{4}{3}$
C. 2
D. 3

A. $\frac{3}{4}$
B. $\frac{4}{3}$
C. 2
D. 3
答案:
B
9.(宜宾中考)如图,已知在直角$\triangle ABC$中,$CD$是斜边$AB$上的高,$AC = 4$,$BC = 3$,则$AD =$________.
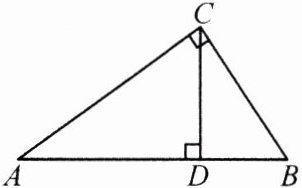

答案:
$\frac{1}{5}$
10.(乐山中考)如图,$E$是矩形$ABCD$的边$CB$上的一点,$AF\perp DE$于点$F$,$AB = 3$,$AD = 2$,$CE = 1$. 求$DF$的长度.
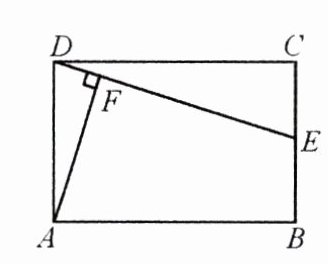

答案:
$\because$四边形$ABCD$是矩形,$\therefore DC = AB = 3$,$\angle ADC=\angle C = 90^{\circ}$,$\because CE = 1$,$\therefore DE=\sqrt{DC^{2}+CE^{2}}=\sqrt{10}$,$\because AF\perp DE$,$\therefore\angle AFD = 90^{\circ}=\angle C$,$\angle ADF+\angle DAF = 90^{\circ}$,又$\because\angle ADF+\angle EDC = 90^{\circ}$,$\therefore\angle EDC=\angle DAF$,$\therefore\triangle EDC\sim\triangle DAF$,$\therefore\frac{DE}{AD}=\frac{CE}{FD}$,即$\frac{\sqrt{10}}{2}=\frac{1}{FD}$,$\therefore FD=\frac{\sqrt{10}}{5}$,即$DF$的长度为$\frac{\sqrt{10}}{5}$
查看更多完整答案,请扫码查看


