《2025年原创新课堂九年级数学下册人教版》

9.如图，以点$O$为位似中心，作四边形$ABCD$的位似图形$A'B'C'D'$，已知$\frac{OA}{OA'} = \frac{1}{3}$，若四边形$ABCD$的面积是2，则四边形$A'B'C'D'$的面积是______.

答案： 18

10.如图，已知$\triangle DEO$与$\triangle ABO$是位似图形，$\triangle OEF$与$\triangle OBC$是位似图形，求证：$OD\cdot OC = OF\cdot OA$.

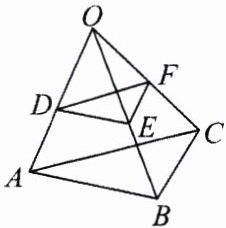
答案： 证明：
∵△DEO与△ABO位似，
∴$\frac{OD}{OA}=\frac{OE}{OB}$。
∵△OEF与△OBC位似，
∴$\frac{OE}{OB}=\frac{OF}{OC}$，
∴$\frac{OD}{OA}=\frac{OF}{OC}$，
∴OD·OC = OF·OA

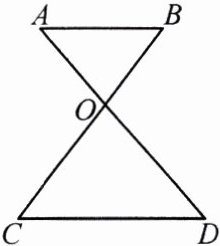
11.如图，$\triangle OAB$与$\triangle ODC$是位似图形，试问：
(1)$AB$与$CD$平行吗？请说明理由；
(2)如果$OB = 3$，$OC = 4$，$OD = 3.5$，试求$\triangle OAB$与$\triangle ODC$的相似比及$OA$的长.

答案： （1）AB//CD。理由：
∵△OAB与△ODC是位似图形，
∴△OAB∽△ODC，
∴∠D = ∠A，
∴AB//CD （2）由题意得点O是位似中心，则△OAB与△ODC的相似比为OB : OC = 3 : 4。
∵△OAB∽△ODC，
∴OB : OC = OA : OD，即3 : 4 = OA : 3.5，
∴OA = 2.625

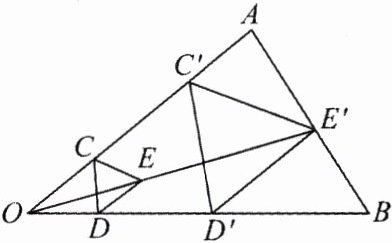
12.如图，用下面的方法可以画$\triangle AOB$的内接等边三角形，阅读后证明相应问题.
画法：①在$\triangle AOB$内画等边$\triangle CDE$使点$C$在$OA$上，点$D$在$OB$上；②连接$OE$并延长，交$AB$于点$E'$，过点$E'$作$E'C'// EC$，交$OA$于点$C'$，作$E'D'// ED$，交$OB$于点$D'$；③连接$C'D'$，则$\triangle C'D'E'$是$\triangle AOB$的内接等边三角形.
求证：$\triangle C'D'E'$是等边三角形.

答案： 证明：
∵E'C'//EC，E'D'//ED，
∴△OCE∽△OC'E'，△ODE∽△OD'E'，
∴CE : C'E' = OE : OE'，DE : D'E' = OE : OE'，∠CEO = ∠C'E'O，∠DEO = ∠D'E'O，
∴CE : C'E' = DE : D'E'，∠CED = ∠C'E'D'，
∴△CDE∽△C'D'E'，
∵△CDE是等边三角形，
∴△C'D'E'是等边三角形

13.(2024·郑州月考)如图，在网格图中，每格是边长为1的正方形，四边形$ABCD$的顶点均在格点上.
(1)请以点$O$为位似中心，在网格图中作出四边形$A'B'C'D'$，使四边形$A'B'C'D'$与四边形$ABCD$位似，且$\frac{OC'}{OC}=2$；
(2)填空：线段$BB'$的长为________，$\triangle A'D'O$的面积为______.

答案：
（1）（2）$6\sqrt{2}$ 10