1.(2024·平顶山宝丰县期末)$\sin60^{\circ}$的值为 ( )
A.$\frac{\sqrt{3}}{2}$
B.$\frac{\sqrt{2}}{2}$
C.1
D.$\frac{1}{2}$
A.$\frac{\sqrt{3}}{2}$
B.$\frac{\sqrt{2}}{2}$
C.1
D.$\frac{1}{2}$
答案:
A
2.$2\tan45^{\circ}$的值等于 ( )
A.1
B.$\frac{\sqrt{2}}{2}$
C.$\sqrt{2}$
D.2
A.1
B.$\frac{\sqrt{2}}{2}$
C.$\sqrt{2}$
D.2
答案:
D
3.计算$\cos^{2}45^{\circ}+\tan60^{\circ}\cos30^{\circ}$的值为____。
答案:
2
4.(教材 P69 习题 3 变式)计算:
(1)$\frac{1}{2}\sin60^{\circ}\times\frac{\sqrt{2}}{2}\cos45^{\circ}$;
(2)$\tan^{2}30^{\circ}-\cos^{2}30^{\circ}-\sin^{2}45^{\circ}\cdot\tan45^{\circ}$;
(3)$\frac{\tan60^{\circ}-\tan45^{\circ}}{\tan60^{\circ}\cdot\tan45^{\circ}}+2\sin60^{\circ}$。
(1)$\frac{1}{2}\sin60^{\circ}\times\frac{\sqrt{2}}{2}\cos45^{\circ}$;
(2)$\tan^{2}30^{\circ}-\cos^{2}30^{\circ}-\sin^{2}45^{\circ}\cdot\tan45^{\circ}$;
(3)$\frac{\tan60^{\circ}-\tan45^{\circ}}{\tan60^{\circ}\cdot\tan45^{\circ}}+2\sin60^{\circ}$。
答案:
- (1)原式 = $\frac{\sqrt{3}}{8}$
- (2)原式 = -$\frac{11}{12}$
- (3)原式 = $1 + \frac{2}{3}\sqrt{3}$
5.(怀化中考)已知$\angle\alpha$为锐角,且$\sin\alpha=\frac{1}{2}$,则$\angle\alpha=$ ( )
A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$90^{\circ}$
A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$90^{\circ}$
答案:
A
6.李红同学遇到了这样一道题:$\sqrt{3}\tan(\alpha + 20^{\circ}) = 1$,则锐角$\alpha$的度数为 ( )
A.$40^{\circ}$
B.$30^{\circ}$
C.$20^{\circ}$
D.$10^{\circ}$
A.$40^{\circ}$
B.$30^{\circ}$
C.$20^{\circ}$
D.$10^{\circ}$
答案:
D
7.在$\triangle ABC$中,$\angle A$,$\angle B$都是锐角,若$\cos A = \frac{\sqrt{3}}{2}$,$\sin B = \frac{1}{2}$,则$\angle C =$______。
答案:
$120^{\circ}$
8.(1)已知$2\sin(\angle A + 13^{\circ}) = 1$,求锐角$A$的度数;
(2)已知$3\tan\alpha - \sqrt{3} = 0$,求锐角$\alpha$的度数。
(2)已知$3\tan\alpha - \sqrt{3} = 0$,求锐角$\alpha$的度数。
答案:
- (1)因为$2\sin(\angle A + 13^{\circ}) = 1$,所以$\sin(\angle A + 13^{\circ}) = \frac{1}{2}$,所以$\angle A + 13^{\circ} = 30^{\circ}$,所以$\angle A = 17^{\circ}$,所以锐角$A$的度数为$17^{\circ}$。
- (2)因为$3\tan\alpha - \sqrt{3} = 0$,所以$\tan\alpha = \frac{\sqrt{3}}{3}$,所以$\alpha = 30^{\circ}$,所以锐角$\alpha$的度数为$30^{\circ}$。
9.(威海中考)若用我们数学课本上采用的科学计算器计算$\sin36^{\circ}18'$,按键顺序正确的是 ( )
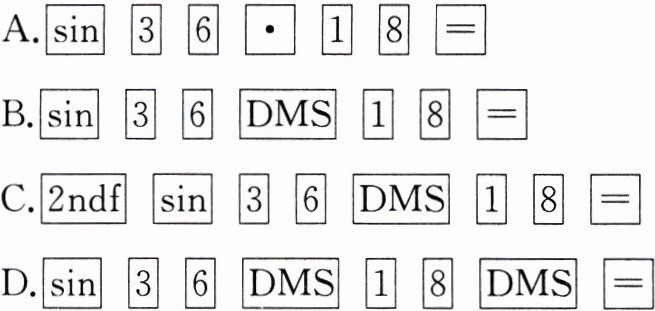
A.$\boxed{\sin}\ \boxed{3}\ \boxed{6}\ \boxed{\cdot}\ \boxed{1}\ \boxed{8}\ \boxed{=}$
B.$\boxed{\sin}\ \boxed{3}\ \boxed{6}\ \boxed{\text{DMS}}\ \boxed{1}\ \boxed{8}\ \boxed{=}$
C.$\boxed{2\text{ndf}}\ \boxed{\sin}\ \boxed{3}\ \boxed{6}\ \boxed{\text{DMS}}\ \boxed{1}\ \boxed{8}\ \boxed{=}$
D.$\boxed{\sin}\ \boxed{3}\ \boxed{6}\ \boxed{\text{DMS}}\ \boxed{1}\ \boxed{8}\ \boxed{\text{DMS}}\ \boxed{=}$

A.$\boxed{\sin}\ \boxed{3}\ \boxed{6}\ \boxed{\cdot}\ \boxed{1}\ \boxed{8}\ \boxed{=}$
B.$\boxed{\sin}\ \boxed{3}\ \boxed{6}\ \boxed{\text{DMS}}\ \boxed{1}\ \boxed{8}\ \boxed{=}$
C.$\boxed{2\text{ndf}}\ \boxed{\sin}\ \boxed{3}\ \boxed{6}\ \boxed{\text{DMS}}\ \boxed{1}\ \boxed{8}\ \boxed{=}$
D.$\boxed{\sin}\ \boxed{3}\ \boxed{6}\ \boxed{\text{DMS}}\ \boxed{1}\ \boxed{8}\ \boxed{\text{DMS}}\ \boxed{=}$
答案:
D
10.式子$2\cos30^{\circ}-\tan45^{\circ}-\sqrt{(1 - \tan60^{\circ})^{2}}$的值是 ( )
A.$2\sqrt{3}-2$
B.0
C.$2\sqrt{3}$
D.2
A.$2\sqrt{3}-2$
B.0
C.$2\sqrt{3}$
D.2
答案:
B
11.在$\triangle ABC$中,已知$\sin A = 0.64$,$\cos B = 0.48$,则$\angle C =$______。(精确到$0.1^{\circ}$)
答案:
$78.9^{\circ}$
12.如图,已知$\odot O$的两条弦$AC$,$BD$相交于点$E$,$\angle A = 70^{\circ}$,$\angle C = 50^{\circ}$,则$\sin\angle AEB$的值为 ( )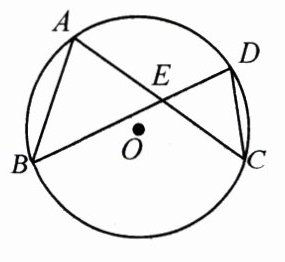
A.$\frac{1}{2}$
B.$\frac{\sqrt{3}}{3}$
C.$\frac{\sqrt{2}}{2}$
D.$\frac{\sqrt{3}}{2}$

A.$\frac{1}{2}$
B.$\frac{\sqrt{3}}{3}$
C.$\frac{\sqrt{2}}{2}$
D.$\frac{\sqrt{3}}{2}$
答案:
D
查看更多完整答案,请扫码查看


