11.(枣庄中考)如图,在半径为 3 的⊙O 中,直径 AB 与弦 CD 相交于点 E,连接 AC,BD,若 AC = 2,则 tanD = ________.
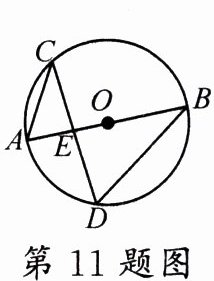

答案:
$2\sqrt{2}$
12.(贵港中考)如图,在 4×4 的网格正方形中,每个小正方形的边长为 1,顶点为格点,若△ABC 的顶点均是格点,则 cos∠BAC 的值是________.
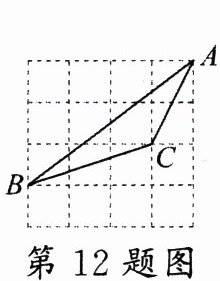

答案:
$\frac{2\sqrt{5}}{5}$
13. 如图,△ABC 中,AB = AC,∠A = 45°,AC 的垂直平分线分别交 AB,AC 于 D,E 两点,连接 CD.如果 AD = 1,那么 tan∠BCD = ________.
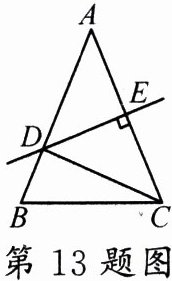

答案:
$\sqrt{2}-1$
14. 如图,AD 是△ABC 的中线,tanB = $\frac{1}{3}$,cosC = $\frac{\sqrt{2}}{2}$,AC = $\sqrt{2}$.求:(1)BC 的长;(2)sin∠ADC 的值.
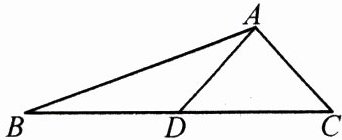

答案:
(1)过点A作AE⊥BC于点E,在Rt△ACE中,
∵$\cos C=\frac{\sqrt{2}}{2}$,$AC=\sqrt{2}$,
∴$CE = AC\cdot\cos C = 1$,
∴$AE=\sqrt{AC^{2}-CE^{2}} = 1$,在Rt△ABE中,$\tan B=\frac{1}{3}$,即$\frac{AE}{BE}=\frac{1}{3}$,
∴$BE = 3AE = 3$,
∴$BC = BE + CE = 4$ (2)
∵AD是△ABC的中线,
∴$CD=\frac{1}{2}BC = 2$,
∴$DE = CD - CE = 1$,在Rt△ADE中,
∴$AD=\sqrt{AE^{2}+DE^{2}}=\sqrt{2}$,
∴$\sin\angle ADC=\frac{AE}{AD}=\frac{\sqrt{2}}{2}$
∵$\cos C=\frac{\sqrt{2}}{2}$,$AC=\sqrt{2}$,
∴$CE = AC\cdot\cos C = 1$,
∴$AE=\sqrt{AC^{2}-CE^{2}} = 1$,在Rt△ABE中,$\tan B=\frac{1}{3}$,即$\frac{AE}{BE}=\frac{1}{3}$,
∴$BE = 3AE = 3$,
∴$BC = BE + CE = 4$ (2)
∵AD是△ABC的中线,
∴$CD=\frac{1}{2}BC = 2$,
∴$DE = CD - CE = 1$,在Rt△ADE中,
∴$AD=\sqrt{AE^{2}+DE^{2}}=\sqrt{2}$,
∴$\sin\angle ADC=\frac{AE}{AD}=\frac{\sqrt{2}}{2}$
15. 如图,将矩形 ABCD 沿 CE 折叠,点 B 恰好落在边 AD 上的点 F 处,如果 $\frac{AB}{BC}$ = $\frac{2}{3}$,求 tan∠DCF 的值.
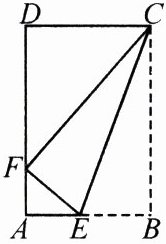

答案:
∵四边形ABCD是矩形,
∴$AB = CD$,∠D = 90°.
∵$\frac{AB}{BC}=\frac{2}{3}$,且由折叠知$CF = BC$,
∴$\frac{CD}{CF}=\frac{2}{3}$. 设$CD = 2x$,$CF = 3x$($x>0$),
∴$DF=\sqrt{CF^{2}-CD^{2}}=\sqrt{5}x$,
∴$\tan\angle DCF=\frac{DF}{CD}=\frac{\sqrt{5}x}{2x}=\frac{\sqrt{5}}{2}$
∵四边形ABCD是矩形,
∴$AB = CD$,∠D = 90°.
∵$\frac{AB}{BC}=\frac{2}{3}$,且由折叠知$CF = BC$,
∴$\frac{CD}{CF}=\frac{2}{3}$. 设$CD = 2x$,$CF = 3x$($x>0$),
∴$DF=\sqrt{CF^{2}-CD^{2}}=\sqrt{5}x$,
∴$\tan\angle DCF=\frac{DF}{CD}=\frac{\sqrt{5}x}{2x}=\frac{\sqrt{5}}{2}$
16. 如图,定义:在直角三角形 ABC 中,锐角α的邻边与对边的比叫做角α的余切,记作 ctanα,即 ctanα = $\frac{角α的邻边}{角α的对边}$ = $\frac{AC}{BC}$,根据上述角的余切定义,解下列问题:
(1)ctan30° = ________;
(2)如图,已知 tanA = $\frac{3}{4}$,其中∠A 为锐角,试求 ctanA 的值.
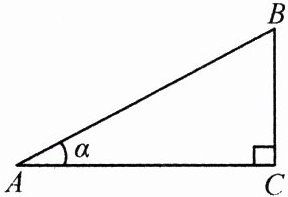
(1)ctan30° = ________;
(2)如图,已知 tanA = $\frac{3}{4}$,其中∠A 为锐角,试求 ctanA 的值.

答案:
$\sqrt{3}$@@
∵$\tan A=\frac{3}{4}$,
∴设$BC = 3x$,$AC = 4x$,
∴$c\tan A=\frac{AC}{BC}=\frac{4x}{3x}=\frac{4}{3}$
∵$\tan A=\frac{3}{4}$,
∴设$BC = 3x$,$AC = 4x$,
∴$c\tan A=\frac{AC}{BC}=\frac{4x}{3x}=\frac{4}{3}$
查看更多完整答案,请扫码查看


