《2025年原创新课堂九年级数学下册人教版》

1.(2024·重庆)已知点(-3,2)在反比例函数$y = \frac{k}{x}(k \neq 0)$的图象上，则$k$的值为 （ ）
A.-3
B.3
C.-6
D.6

答案： C

2.若$A(3,1),B(m,4)$均为反比例函数图象上的点，那么$m =$_______.

答案： $\frac{3}{4}$

3.(2024·湘潭)如图，平面直角坐标系中，$O$是坐标原点，点$A$是反比例函数$y = \frac{k}{x}(k \neq 0)$图象上的一点，过点$A$分别作$AM \perp x$轴于点$M$，$AN \perp y$轴于点$N$，若四边形$AMON$的面积为2.则$k$的值是 （ ）

A.2
B.-2
C.1
D.-1

答案： A

4.(2024·长沙)如图，在平面直角坐标系中，点$A$在反比例函数$y = \frac{k}{x}(k$为常数，$k ＞ 0,x ＞ 0)$的图象上，过点$A$作$x$轴的垂线，垂足为$B$，连接$OA$.若$\triangle OAB$的面积为$\frac{19}{12}$，则$k =$______.

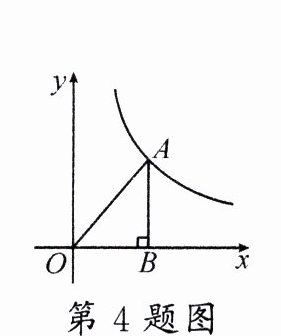
答案： $\frac{19}{6}$

5.(2024·齐齐哈尔)如图，点$A$在反比例函数$y = \frac{k}{x}$图象的一支上，点$B$在反比例函数$y = -\frac{k}{2x}$图象的一支上，点$C,D$在$x$轴上，若四边形$ABCD$是面积为9的正方形，则实数$k$的值为______.

答案： -6

6.(2024·安徽)已知反比例函数$y = \frac{k}{x}(k \neq 0)$与一次函数$y = 2 - x$的图象的一个交点的横坐标为3，则$k$的值为 （ ）
A.-3
B.-1
C.1
D.3

答案： A

7.(2024·威海)如图，在平面直角坐标系中，直线$y_1 = ax + b(a \neq 0)$与双曲线$y_2 = \frac{k}{x}(k \neq 0)$交于点$A(-1,m),B(2,-1)$.则满足$y_1 \leq y_2$的$x$的取值范围________________.

答案： $-1\leqslant x\lt0$或$x\geqslant2$

8.(2024·安阳滑县月考)如图，正比例函数$y = kx$与函数$y = \frac{5}{x}$的图象交于$A,B$两点，$BC // x$轴，$AC // y$轴，则$S_{\triangle ABC} =$______.

答案： 10

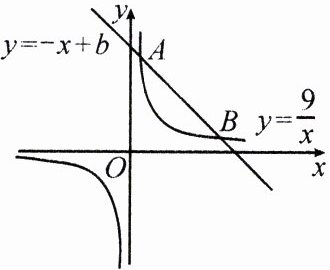
9.(2024·青海)如图，在同一平面直角坐标系中，一次函数$y = -x + b$和反比例函数$y = \frac{9}{x}$的图象相交于点$A(1,m),B(n,1)$.
(1)求点$A$，点$B$的坐标及一次函数的解析式；
(2)根据图象，直接写出不等式$-x + b ＞ \frac{9}{x}$的解集.

答案：
(1)把点$A(1,m)$代入$y = \frac{9}{x}$中，得$m = 9$，
∴点$A$的坐标为$(1,9)$，把点$B(n,1)$代入$y = \frac{9}{x}$中，得$n = 9$，
∴点$B$的坐标为$(9,1)$，把$(1,9)$代入$y = -x + b$中，得$-1 + b = 9$，$b = 10$，
∴一次函数的解析式为$y = -x + 10$
(2)根据一次函数和反比例函数图象，可得$-x + b\gt\frac{9}{x}$的解集为$x\lt0$或$1\lt x\lt9$