《2025年PASS教材搭档七年级数学上册鲁教版》

类型1 点的坐标与象限之间的关系
例1 点$(-2, 1)$所在的象限是(B)

A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： 规范解答:因为点$(-2, 1)$的横坐标小于$0$，纵坐标大于$0$，所以点$(-2, 1)$位于第二象限。
答案:B
类题巧解
熟练掌握各象限内点的坐标的符号特点是解题的关键。各象限内点的坐标的符号特点可以记为“一$(+, +)$，二$(-, +)$，三$(-, -)$，四$(+, -)$”。

类型2 根据点的坐标描点、连线构成图形
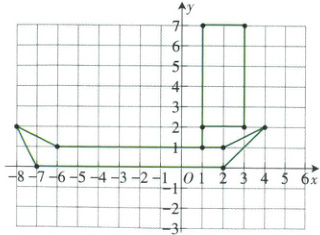
例2 在如图所示的平面直角坐标系内，描出下列各组点，并将各组内的点依次用线段连接起来。
第一组:$(-8, 2)$，$(-6, 1)$，$(2, 1)$，$(4, 2)$，$(2, 0)$，$(-7, 0)$，$(-8, 2)$；
第二组:$(1, 1)$，$(1, 7)$，$(3, 7)$，$(3, 2)$，$(1, 2)$。
观察所得到的图形，你觉得它像什么？

答案： 规范解答:描点、连线，如上图所示。
观察可知，该图形像一条船。
类题巧解
解决此类问题的关键是描点准确。此外连线时注意顺次连接各组内的点。

类型3 平面直角坐标系与平面图形的综合应用
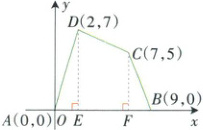
例3 在如图所示的平面直角坐标系中，四边形$ABCD$的各顶点的坐标分别是$A(0, 0)$，$B(9, 0)$，$C(7, 5)$，$D(2, 7)$，求这个四边形的面积。

答案： 规范解答:如上图，过点$D$，$C$分别向$x$轴作垂线，垂足分别为$E$，$F$。
观察可知，四边形$ABCD$被分割为$\triangle AED$，$\triangle BCF$及梯形$CDEF$。
由各点坐标可知，$AE = 2$，$DE = 7$，$EF = 7 - 2 = 5$，$FB = 9 - 7 = 2$，$CF = 5$，
则$S_{\triangle AED} = \frac{1}{2}AE · DE = \frac{1}{2} × 2 × 7 = 7$，
$S_{\triangle BCF} = \frac{1}{2}FB · CF = \frac{1}{2} × 2 × 5 = 5$，
$S_{梯形CDEF} = \frac{1}{2}(DE + CF) · EF = \frac{1}{2} × (7 + 5) × 5 = 30$。
所以$S_{四边形ABCD} = S_{\triangle AED} + S_{\triangle BCF} + S_{梯形CDEF} = 7 + 5 + 30 = 42$。
类题巧解
(1)通过线段长可以求点的坐标，知道点的坐标可以求点到坐标轴的距离。
(2)在平面直角坐标系中求多边形的面积时，一般采用割补法，将其割补为规则图形，再利用已知点的坐标求出有关线段的长度，从而求出面积。