2025年PASS教材搭档七年级数学上册鲁教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年PASS教材搭档七年级数学上册鲁教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
例 铁路施工人员在建设某铁路的过程中,需要打通一座小山,如右图。设计时要测量隧道的长度,恰好在山的前面是一片空地,利用这样的有利地形,测量人员是否可以利用三角形全等的知识测量出需要开挖隧道的长度呢?请画出你设计的测量方法图,并说明理由。


答案:
规范解答:可以。画出示意图(如右图),在山前的空地上任选一点$O$,山脚两点分别为$A,B$。连接$AO,BO$,并分别延长至点$D,C$,使$AO = DO,BO = CO$,连接$CD$,测得$CD$的长度即为开挖隧道的长度。
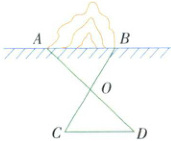
理由如下:
在$\triangle AOB$与$\triangle DOC$中,
因为$AO = DO,\angle AOB = \angle DOC,BO = CO$,
所以$\triangle AOB \cong \triangle DOC(SAS)$,
所以$AB = CD$,
即测得$CD$的长度就是开挖隧道的长度。
规范解答:可以。画出示意图(如右图),在山前的空地上任选一点$O$,山脚两点分别为$A,B$。连接$AO,BO$,并分别延长至点$D,C$,使$AO = DO,BO = CO$,连接$CD$,测得$CD$的长度即为开挖隧道的长度。

理由如下:
在$\triangle AOB$与$\triangle DOC$中,
因为$AO = DO,\angle AOB = \angle DOC,BO = CO$,
所以$\triangle AOB \cong \triangle DOC(SAS)$,
所以$AB = CD$,
即测得$CD$的长度就是开挖隧道的长度。
类型 1 利用三角形全等测距离
例1 如图,$A,B$是位于河两岸的两个建筑物,请你运用三角形全等的知识测出$A,B$两个建筑物之间的距离,并说明理由。
例1 如图,$A,B$是位于河两岸的两个建筑物,请你运用三角形全等的知识测出$A,B$两个建筑物之间的距离,并说明理由。

答案:
规范解答:测量方法如图:
(1)从$B$点出发沿河岸画出一条射线$BF$,在$BF$上截
取$BC = CD$;
(2)过点$D$作$DE // AB$,使$E,C,A$三点在同一条直线上;
(3)测得$ED$的长度就是$A,B$两个建筑物之间的距离。
理由如下:
根据题意以及测量的方法知,$CB = CD,\angle ACB = \angle ECD$。
因为$AB // DE$,
所以$\angle ABC = \angle EDC$。
在$\triangle ABC$和$\triangle EDC$中,
因为$\angle ABC = \angle EDC,CB = CD,\angle ACB = \angle ECD$,
所以$\triangle ABC \cong \triangle EDC(ASA)$,
所以$AB = ED$。
因此,测得$ED$的长度就是$A,B$两个建筑物之间的距离。

规范解答:测量方法如图:
(1)从$B$点出发沿河岸画出一条射线$BF$,在$BF$上截
取$BC = CD$;
(2)过点$D$作$DE // AB$,使$E,C,A$三点在同一条直线上;
(3)测得$ED$的长度就是$A,B$两个建筑物之间的距离。
理由如下:
根据题意以及测量的方法知,$CB = CD,\angle ACB = \angle ECD$。
因为$AB // DE$,
所以$\angle ABC = \angle EDC$。
在$\triangle ABC$和$\triangle EDC$中,
因为$\angle ABC = \angle EDC,CB = CD,\angle ACB = \angle ECD$,
所以$\triangle ABC \cong \triangle EDC(ASA)$,
所以$AB = ED$。
因此,测得$ED$的长度就是$A,B$两个建筑物之间的距离。

查看更多完整答案,请扫码查看


