2025年PASS教材搭档七年级数学上册鲁教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年PASS教材搭档七年级数学上册鲁教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
例1 如图,$\triangle ABH$,$\triangle BCG$,$\triangle CDF$和$\triangle DAE$是四个全等的直角三角形,四边形$ABCD$和四边形$EFGH$都是正方形,如果$AB = 10$,$AH = 6$,那么$EF =$
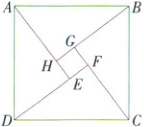
思路分析:由题意知$EF = HG$,$BG = AH$,则在$ Rt \bigtriangleup ABH$中,由$AB^{2}=AH^{2}+HB^{2}$可求得$HB$的长,进而求出$EF$的长。
2
。
思路分析:由题意知$EF = HG$,$BG = AH$,则在$ Rt \bigtriangleup ABH$中,由$AB^{2}=AH^{2}+HB^{2}$可求得$HB$的长,进而求出$EF$的长。
答案:
规范解答:因为$\triangle ABH \cong \triangle BCG$,
所以$AH = BG = 6$。
因为四边形$EFGH$是正方形,
所以$AH \bot BH$,$EF = HG$。
在$ Rt \bigtriangleup ABH$中,由勾股定理,得$AB^{2}=AH^{2}+HB^{2}$,
即$10^{2}=6^{2}+HB^{2}$,所以$HB = 8$,
所以$EF = HG = HB - BG = 8 - 6 = 2$。
答案:2
所以$AH = BG = 6$。
因为四边形$EFGH$是正方形,
所以$AH \bot BH$,$EF = HG$。
在$ Rt \bigtriangleup ABH$中,由勾股定理,得$AB^{2}=AH^{2}+HB^{2}$,
即$10^{2}=6^{2}+HB^{2}$,所以$HB = 8$,
所以$EF = HG = HB - BG = 8 - 6 = 2$。
答案:2
例2 如图所示,有一张直角三角形
纸片$ABC$,其中$AC = 6\ cm$,$BC = 8\ cm$,现将直角边$AC$沿$AD$折叠,使点$C$落在斜边$AB$上的点$E$处,试求$CD$的长。

思路分析:根据勾股定理很容易求出斜边$AB$的长,由折叠的性质可知,$\angle DEA = \angle C = 90^{\circ}$,$AE = AC = 6\ cm$,$CD = DE$,可在$ Rt \bigtriangleup BDE$中求出$DE$,从而求得$CD$的长。
纸片$ABC$,其中$AC = 6\ cm$,$BC = 8\ cm$,现将直角边$AC$沿$AD$折叠,使点$C$落在斜边$AB$上的点$E$处,试求$CD$的长。

思路分析:根据勾股定理很容易求出斜边$AB$的长,由折叠的性质可知,$\angle DEA = \angle C = 90^{\circ}$,$AE = AC = 6\ cm$,$CD = DE$,可在$ Rt \bigtriangleup BDE$中求出$DE$,从而求得$CD$的长。
答案:
规范解答:在$ Rt \bigtriangleup ABC$中,$AC = 6\ cm$,$BC = 8\ cm$,
由勾股定理,得$AB^{2}=AC^{2}+BC^{2}=6^{2}+8^{2}=100$,
所以$AB = 10\ cm$。
由折叠可知,$\angle DEA = \angle C = 90^{\circ}$,$AE = AC = 6\ cm$,$CD = DE$,
所以$BE = AB - AE = 10 - 6 = 4( cm)$。
设$CD = x\ cm$,则$DE = x\ cm$,$BD = (8 - x) cm$,
在$ Rt \bigtriangleup BDE$中,由勾股定理,得$DE^{2}+BE^{2}=BD^{2}$,即$x^{2}+4^{2}=(8 - x)^{2}$,解得$x = 3$。
所以$CD$的长为$3\ cm$。
由勾股定理,得$AB^{2}=AC^{2}+BC^{2}=6^{2}+8^{2}=100$,
所以$AB = 10\ cm$。
由折叠可知,$\angle DEA = \angle C = 90^{\circ}$,$AE = AC = 6\ cm$,$CD = DE$,
所以$BE = AB - AE = 10 - 6 = 4( cm)$。
设$CD = x\ cm$,则$DE = x\ cm$,$BD = (8 - x) cm$,
在$ Rt \bigtriangleup BDE$中,由勾股定理,得$DE^{2}+BE^{2}=BD^{2}$,即$x^{2}+4^{2}=(8 - x)^{2}$,解得$x = 3$。
所以$CD$的长为$3\ cm$。
例3 葛藤是一种多年生草质藤本植物,为获得更多的雨露和阳光,其茎蔓常绕着附近的树干盘旋而上。若把树干看成圆柱体,则它的底面周长为$3$尺,现有一段葛藤绕树干盘旋一周后升高$4$尺,则这段葛藤盘旋的最短距离是(尺是我国市制长度单位$)$ ()
A.$3$尺
B.$4$尺
C.$5$尺
D.$6$尺
思路分析:将立体图形展开成平面图形,构造直角三角形,再利用勾股定理求解。
A.$3$尺
B.$4$尺
C.$5$尺
D.$6$尺
思路分析:将立体图形展开成平面图形,构造直角三角形,再利用勾股定理求解。
答案:
规范解答:示意图如图,由题意可知$AB = 3$尺,$BC = 4$尺。在$ Rt \bigtriangleup ABC$中,由勾股定理,得$AC^{2}=AB^{2}+BC^{2}=25 = 5^{2}$,所以$AC = 5$尺,故这段葛藤盘旋的最短距离是$5$尺。

答案:C
规范解答:示意图如图,由题意可知$AB = 3$尺,$BC = 4$尺。在$ Rt \bigtriangleup ABC$中,由勾股定理,得$AC^{2}=AB^{2}+BC^{2}=25 = 5^{2}$,所以$AC = 5$尺,故这段葛藤盘旋的最短距离是$5$尺。

答案:C
例4 小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多了$1\ m$,当他把绳子下端拉开$5\ m$后,发现下端刚好与地面接触,求旗杆的高度。

思路分析:根据题意画出图形,再根据勾股定理求解。

思路分析:根据题意画出图形,再根据勾股定理求解。
答案:
规范解答:根据题意画出图形如图。

设旗杆高$AB$为$x\ m$,则绳长$AC = (x + 1) m$。
在$ Rt \bigtriangleup ABC$中,由勾股定理,得$AB^{2}+BC^{2}=AC^{2}$,
即$x^{2}+5^{2}=(x + 1)^{2}$,解得$x = 12$。
故旗杆的高度为$12\ m$。
规范解答:根据题意画出图形如图。

设旗杆高$AB$为$x\ m$,则绳长$AC = (x + 1) m$。
在$ Rt \bigtriangleup ABC$中,由勾股定理,得$AB^{2}+BC^{2}=AC^{2}$,
即$x^{2}+5^{2}=(x + 1)^{2}$,解得$x = 12$。
故旗杆的高度为$12\ m$。
查看更多完整答案,请扫码查看


