《2025年名校课堂九年级数学全一册鲁教版五四制山东专版》

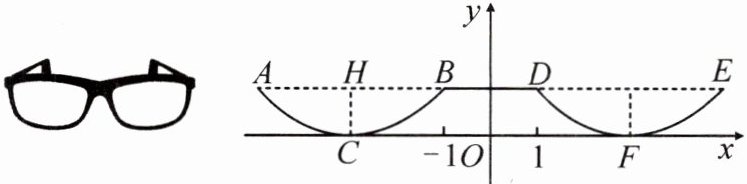
9. 【真实问题情境】(东营利津县期中)如图,这是一副眼镜镜片下半部分轮廓对应的两条抛物线,它们关于 $ y $ 轴对称,$ AB // x $ 轴,$ AB = 4 $ cm,最低点 $ C $ 在 $ x $ 轴上,高 $ CH = 1 $ cm,$ BD = 2 $ cm,则右轮廓线 $ DFE $ 所在抛物线的函数表达式为$y = \frac { 1 } { 4 } ( x - 3 ) ^ { 2 }$(不用写 $ x $ 的取值范围).

答案： 9.$y = \frac { 1 } { 4 } ( x - 3 ) ^ { 2 }$

10. (淄博期末)如图,隧道的截面由抛物线和长方形构成,长方形的长是 $ 12 $ m,宽是 $ 4 $ m.按照图中所示的平面直角坐标系,抛物线可以用 $ y = -\frac{1}{6}x^2 + bx + c $ 表示,且抛物线的点 $ C $ 到墙面 $ OB $ 的水平距离为 $ 3 $ m 时,到地面 $ OA $ 的距离为 $ \frac{17}{2} $ m.
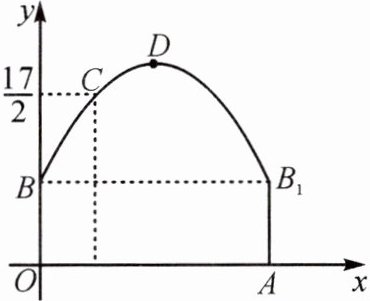
(1)求该抛物线的函数关系式,并计算出拱顶 $ D $ 到地面 $ OA $ 的距离;
(2)一辆货运汽车载一长方体集装箱后高为 $ 6 $ m,宽为 $ 4 $ m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过 $ 8 $ m,那么两排灯的水平距离最小是$4 \sqrt { 3 }$m.

答案： 10.
(1)抛物线的表达式为$y = - \frac { 1 } { 6 } x ^ { 2 } + 2 x + 4$，拱顶$D$到地面$OA$的距离为$10 \text { m }$；
(2)这辆货车能安全通过；
(3)$4 \sqrt { 3 }$

11. (绍兴中考)如图 1,排球场长为 $ 18 $ m,宽为 $ 9 $ m,网高为 $ 2.24 $ m,队员站在底线 $ O $ 点处发球,球从点 $ O $ 的正上方 $ 1.9 $ m 的 $ C $ 点发出,运动路线是抛物线的一部分,当球运动到最高点 $ A $ 时,高度为 $ 2.88 $ m,即 $ BA = 2.88 $ m,这时水平距离 $ OB = 7 $ m,以直线 $ OB $ 为 $ x $ 轴,直线 $ OC $ 为 $ y $ 轴,建立平面直角坐标系,如图 2.
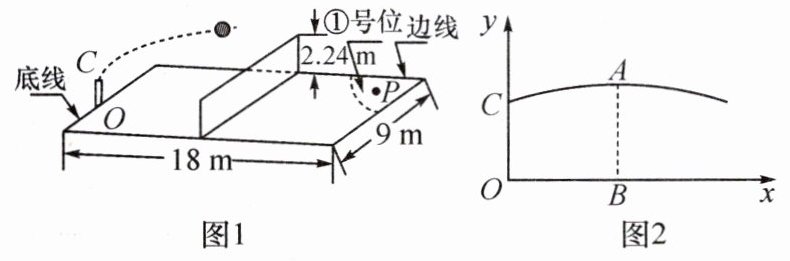
(1)若球向正前方运动(即 $ x $ 轴垂直于底线),求球运动的高度 $ y $(m)与水平距离 $ x $(m)之间的函数关系式(不必写出 $ x $ 取值范围).并判断这次发球能否过网?是否出界?说明理由;
(2)若球过网后的落点是对方场地①号位内的点 $ P $(如图 1,点 $ P $ 距底线 $ 1 $ m,边线 $ 0.5 $ m),问发球点 $ O $ 在底线上的哪个位置? (参考数据:$ \sqrt{2} $ 取 $ 1.4 $)

答案： 11.
(1)抛物线的表达式为$y = - \frac { 1 } { 50 } ( x - 7 ) ^ { 2 } + 2.88$，这次发球过网，但是出界了；
(2)发球点$O$在底线上且距右边线$0.1 \text { m }$处.