《2025年名校课堂九年级数学全一册鲁教版五四制山东专版》

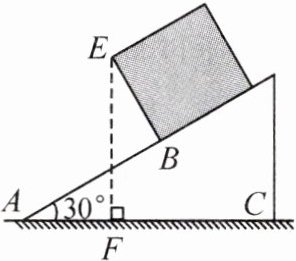
8. 一个长方体木箱沿斜面下滑，当木箱滑至如图位置时，$ AB = 3\ m $，已知木箱高 $ BE = \sqrt{3}\ m $，斜面坡角为 $ 30^{\circ} $，则木箱端点 $ E $ 距地面 $ AC $ 的高度为3 m.

答案： 8.3 m

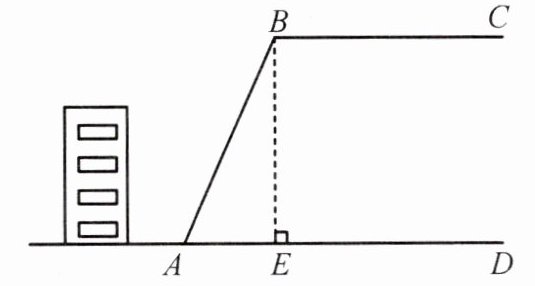
9. (泰安中考)如图，某校教学楼后面紧邻着一个山坡，坡上面是一块平地. $ BC // AD $，$ BE \perp AD $，斜坡 $ AB $ 长 $ 26\ m $，斜坡 $ AB $ 的坡比为 $ 12:5 $. 为了减缓坡面，防止山体滑坡，学校决定对该斜坡进行改造. 经地质人员勘测，当坡角不超过 $ 50^{\circ} $ 时，可确保山体不滑坡. 如果改造时保持坡脚 $ A $ 不动，则坡顶 $ B $ 沿 $ BC $ 至少向右移10$m$ 时，才能确保山体不滑坡.(取 $ \tan 50^{\circ} \approx 1.2 $)

答案： 9.10

10. (淄博中考改编)如图，与斜坡 $ CE $ 垂直的太阳光线照射立柱 $ AB $（与水平地面 $ BF $ 垂直）形成的影子，一部分落在地面上，另一部分落在斜坡上. 若 $ BC = 2 $ 米，$ CD = 8.48 $ 米，斜坡的坡角 $ \angle ECF = 32^{\circ} $，求立柱 $ AB $ 的高.（结果精确到 $ 0.1 $ 米）

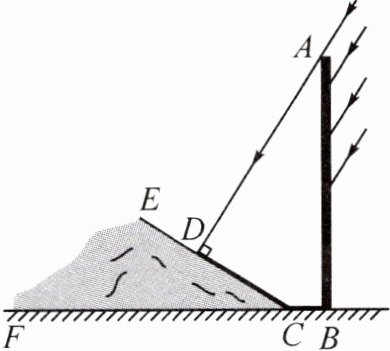
答案： 10.解：延长AD交BF于点H．在Rt△CDH中，CD = 8.48米，∠DCH = 32°，$\cos\angle DCH = \frac{CD}{CH}，$
∴$CH = \frac{CD}{\cos\angle DCH}≈\frac{8.48}{0.848}= 10($米)．
∴BH = CH + BC = 10 + 2 = 12(米)．
∵∠DCH =90°，∠DCH = 32°，
∴∠DHC = 90° - ∠DCH = 58°．
∵AB⊥BF，
∴∠BAH = 90° - ∠DHC = 32°．在Rt△ABH中，$\tan\angle BAH = \frac{BH}{AB}，$
∴$AB = \frac{BH}{\tan\angle BAH}≈\frac{12}{0.625} = 19.2($米)．答：立柱AB的高约为19.2米．

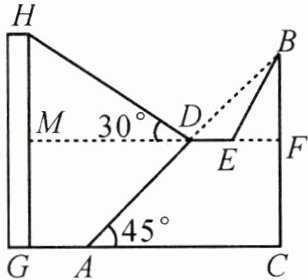
11. (广安中考)广安市政府对城市建设进行了整改. 如图，已知斜坡 $ AB $ 长 $ 60\sqrt{2} $ 米，坡角（即 $ \angle BAC $）为 $ 45^{\circ} $，$ BC \perp AC $，现计划在斜坡中点 $ D $ 处挖去部分斜坡，修建一个平行于水平线 $ CA $ 的休闲平台 $ DE $ 和一条新的斜坡 $ BE $.（下面两个小题结果都保留根号）
(1) 若修建的斜坡 $ BE $ 的坡比为 $ \sqrt{3}:1 $，求休闲平台 $ DE $ 的长是多少米；
(2) 一座建筑物 $ GH $ 距离 $ A $ 点 33 米远（即 $ AG = 33 $ 米），小亮在 $ D $ 点测得建筑物顶部 $ H $ 的仰角（即 $ \angle HDM $）为 $ 30^{\circ} $. 点 $ B $，$ C $，$ A $，$ G $，$ H $ 在同一个平面内，点 $ C $，$ A $，$ G $ 在同一条直线上，且 $ HG \perp CG $，问建筑物 $ GH $ 高为多少米？

答案： 11.解：
(1)
∵BC⊥AC，∠BAC = 45°，DE//AC，
∴AC = BC，DF =BF．
∵$AB = 60\sqrt{2}$米，
∴AC = BC = 60米．
∵D是AB的中点，
∴$AD = BD = 30\sqrt{2}$米．
∴BF = DF = 30米．
∵BE的坡比为$\sqrt{3}:1，$
∴$EF = \frac{BF}{\sqrt{3}} = \frac{30}{\sqrt{3}} = 10\sqrt{3}($米)．
∴$DE = DF - EF = (3010\sqrt{3})$米．答：休闲平台DE的长为$(30 - 10\sqrt{3})$米．
(2)过点D作DP⊥AC于点P，则四边形GPDM为矩形．
∵$AD = 30\sqrt{2}$米，∠DAP = 45°，
∴AP = DP = GM = 30米．
∴MD = GP =33 + 30 = 63(米)．
∵$\tan\angle HDM = \frac{HM}{MD}，$即$\frac{HM}{63} = \frac{\sqrt{3}}{3}，$
∴$HM =\frac{63\sqrt{3}}{3} = 21\sqrt{3}($米)．
∴$GH = GM + HM = (30 + 21\sqrt{3})$米．答：建筑物GH高为$(30 + 21\sqrt{3})$米．