《2025年名校课堂九年级数学全一册鲁教版五四制山东专版》

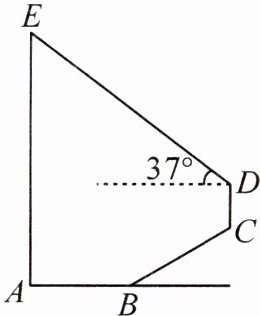
6. 如图，某数学活动小组为测量学校旗杆AE的高度，沿旗杆正前方$2\sqrt{3}$米的点B处出发，沿斜面坡度$i = 1:\sqrt{3}$的斜坡BC前进4米到达点C，在点C处安置测角仪，测得旗杆顶部E的仰角为$37^{\circ}$，量得仪器的高CD为$1.5$米。已知点A，B，C，D，E在同一平面内，$AE \perp AB$，$AE // CD$，则旗杆AE的高度是8.7米。(结果精确到$0.1$米。参考数据：$\sin37^{\circ} \approx \frac{3}{5}$，$\cos37^{\circ} \approx \frac{4}{5}$，$\tan37^{\circ} \approx \frac{3}{4}$，$\sqrt{3} \approx 1.73$)。

答案： 6.8.7

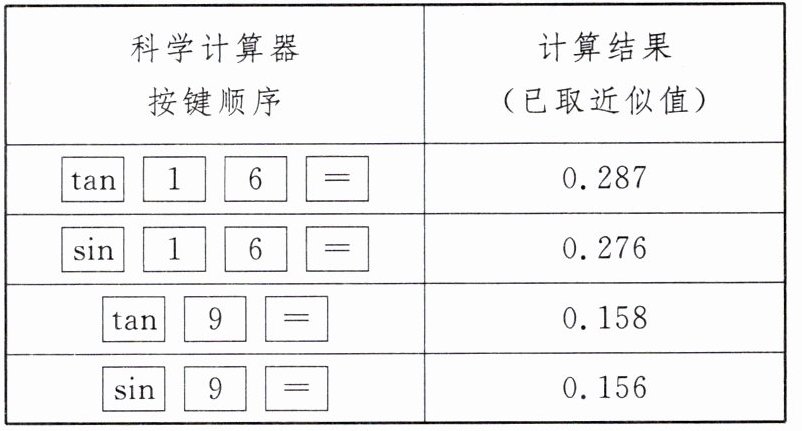
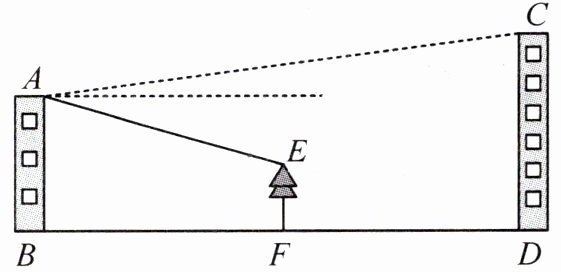
7. (淄博中考)如图，希望中学的教学楼AB和综合楼CD之间生长着一棵高度为$12.88$米的白杨树EF，且其底端点B，D，F在同一条直线上，$BF = FD = 40$米。在综合实践活动课上，小明打算借助这棵树的高度测算出综合楼的高度，他在教学楼顶A处测得点C的仰角为$9^{\circ}$，点E的俯角为$16^{\circ}$。问小明能否运用以上数据，得到综合楼的高度？若能，请求出其高度（结果精确到$0.01$米）；若不能，说明理由。解答过程中可直接选用表格中的数据哟！

答案： 7.解：小明能运用以上数据，得到综合楼的高度.理由如下：作 EG ⊥ AB，垂足为 G，作 AH ⊥ CD，垂足为 H，由题意可知，EG = BF = 40 米，EF = BG = 12.88 米， ∠HAE = ∠AEG = 16°， ∠CAH = 9°。在 Rt△AEG 中，$tan ∠AEG = \frac{AG}{EG}，$
∴ AG = EG · tan ∠AEG ≈ 40 × 0.287 = 11.48(米)。
∴ AB = AG + BG = 11.48 + 12.88 = 24.36(米)。
∴ HD = AB = 24.36 米。在 Rt△ACH 中，AH = BD = BF + FD = 80 米，$tan ∠CAH = \frac{CH}{AH}，$
∴ CH = AH · tan ∠CAH ≈ 80 × 0.158 = 12.64(米)。
∴ CD = CH + HD = 12.64 + 24.36 = 37.00(米)。答：综合楼的高度约是 37.00 米。

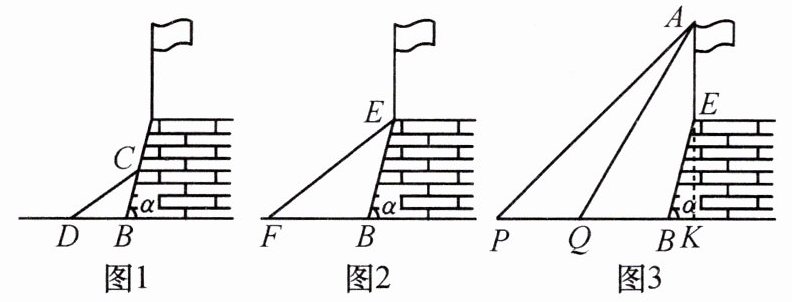
8. (绍兴中考改编)九(1)班同学在上学期的社会实践活动中，对学校旁边的山坡护墙和旗杆进行了测量。
(1)如图1，第一小组用一根木条CD斜靠在护墙上，使得DB与CB的长度相等，如果测量得到∠CDB=$38^{\circ}$，则护墙与地面的倾斜角α的度数为76°；
(2)如图2，第二小组用皮尺量得EF的中点离地面FB的高度为$1.9$米，则点E离地面FB的高度为3.8米；
(3)如图3，第三小组利用第一、第二小组的结果，来测量护墙上旗杆的高度，在点P处测得旗杆顶端A的仰角为$45^{\circ}$，向前走4米到达Q点，测得A的仰角为$60^{\circ}$，求旗杆AE的高度。(结果精确到$0.1$米，参考数据：$\tan60^{\circ} \approx 1.732$，$\tan30^{\circ} \approx 0.577$，$\sqrt{3} \approx 1.732$，$\sqrt{2} \approx 1.414$)

答案： 8.解：
(1)76
(2)3.8
(3)延长 AE 交 PB 于点 K，设 AE = x，则 AK = x + 3.8。
∵ ∠APB = 45°，
∴ PK = AK = x + 3.8。
∵ PQ = 4，
∴ KQ = x + 3.8 - 4 = x - 0.2。
∵$ tan ∠AQK = \frac{AK}{QK} = tan60° = \sqrt{3}，$
∴$ \frac{x + 3.8}{x - 0.2} = \sqrt{3}。$解得$ x = \frac{3.8 + \frac{1}{5}\sqrt{3}}{\sqrt{3} - 1} ≈ 5.7。$答：旗杆 AE 的高度约为 5.7 米。