《2025年名校课堂九年级数学全一册鲁教版五四制山东专版》

9. (咸宁中考) 用一根长为 40 cm 的绳子围成一个面积为 $a$ cm² 的长方形, 那么 $a$ 的值不可能为 (D)

A.20
B.40
C.100
D.120

答案： 9.D

10. 如图, 在 $Rt\triangle ABC$ 中, $AC = 3$ cm, $BC = 4$ cm, 四边形 CFDE 为矩形, 其中 CF, CE 在两直角边上. 设矩形的一边 $CF = x$ cm, 当 $x =$ 2 时, 矩形 CFDE 的面积 $S$ 最大, 最大面积是 3 cm².

答案： 10.2 3 cm²

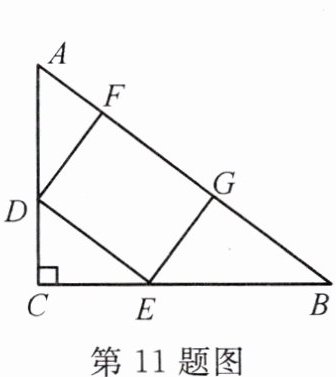
11. (本课时 T10 变式) 如图, 在 $Rt\triangle ABC$ 中, 作一个矩形 DEGF, 其中 FG 在斜边 AB 上, $AC = 3$ cm, $BC = 4$ cm, 则矩形 DEGF 的最大面积是 3 cm².

答案： 11.3 cm²

12. (本课时 T10 变式) 如图, 在 $\triangle ABC$ 中, 矩形 GDEF 的边 DE 在边 BC 上, 点 G, F 分别在边 AB, AC 上, $BC = 5$ cm, $S_{\triangle ABC} = 30$ cm², AH 为 $\triangle ABC$ 的边 BC 上的高, 则矩形 GDEF 的最大面积是 15 cm².

答案： 12.15 cm²

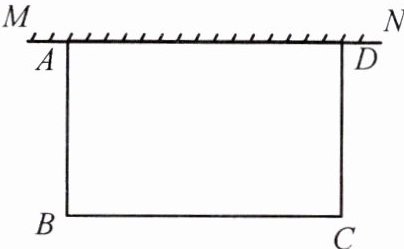
13. (福建中考) 如图, 在足够大的空地上有一段长为 $a$ m 的旧墙 MN, 某人利用旧墙和木栏围成一个矩形菜园 ABCD, 其中 $AD \leq MN$, 已知矩形菜园的一边靠墙, 另三边一共用了 100 m 木栏.
(1) 若 $a = 20$, 所围成的矩形菜园的面积为 450 m², 求所利用旧墙 AD 的长;
(2) 求矩形菜园 ABCD 面积的最大值.

答案： 13.解：
(1)设AB=xm，则BC=(100-2x)m.根据题意，得x(100-2x)=450，解得x₁=5，x₂=45.当x=5时，100-2x=90＞20，不合题意舍去；当x=45时，100-2x=10.答：AD的长为10m.
(2)设AD=xm，
∴$S=\frac{1}{2}x(100-x)=-\frac{1}{2}(x - 50)^{2}+1250.$当a≥50时，则x=50时，S的最大值为1250；当0＜a＜50时，则当0＜x≤a时，S随x的增大而增大，当x=a时，S的最大值为$50a-\frac{1}{2}a².$综上所述，当a≥50时，S的最大值为1250m²；当0＜a＜50时，S的最大值为$(50a-\frac{1}{2}a²)m².$

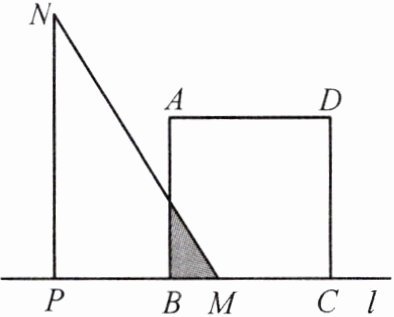
14. (朝阳中考) 如图, 正方形 ABCD 的边长为 2 cm, $\triangle PMN$ 是一块直角三角板 ($\angle N = 30^{\circ}$), $PM ＞ 2$ cm, PM 与 BC 均在直线 $l$ 上, 开始时 M 点与 B 点重合, 将三角板向右平行移动, 直至 M 点与 C 点重合为止. 设 $BM = x$ cm, 三角板与正方形重叠部分的面积为 $y$ cm².
下列结论:
① 当 $0 \leq x \leq \frac{2}{3}\sqrt{3}$ 时, $y$ 与 $x$ 之间的函数关系式为 $y = \frac{\sqrt{3}}{2}x^{2}$;
② 当 $\frac{2}{3}\sqrt{3} ＜ x \leq 2$ 时, $y$ 与 $x$ 之间的函数关系式为 $y = 2x - \frac{2}{3}\sqrt{3}$;
③ 当 MN 经过 AB 的中点时, $y = \frac{1}{2}\sqrt{3}$ cm²;
④ 存在 $x$ 的值, 使 $y = \frac{1}{2}S_{正方形ABCD}$ ($S_{正方形ABCD}$ 表示正方形 ABCD 的面积).
其中正确的是 ①②④ (写出所有正确结论的序号).

答案： 14.①②④