《2025年名校课堂九年级数学全一册鲁教版五四制山东专版》

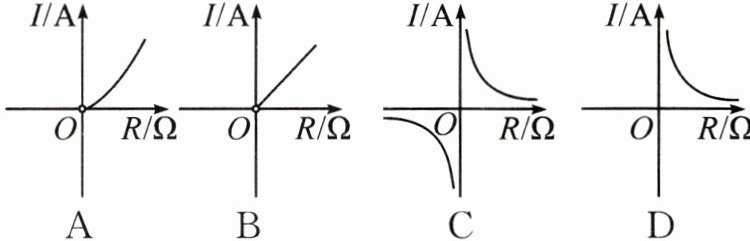
1. 【跨学科问题】(荆州中考)已知蓄电池的电压 $ U $ 为定值，使用蓄电池时，电流 $ I $($ A $) 与电阻 $ R $($ \Omega $) 是反比例函数关系($ I = \frac{U}{R} $)。下列反映电流 $ I $ 与电阻 $ R $ 之间函数关系的图象大致是(D)

]

答案： 1.D

2. 在一个可以改变容积的密闭容器内，装有一定质量 $ m $ 的某种气体，当改变容积 $ V $ 时，气体的密度 $ \rho $ 也随之改变，$ \rho $ 与 $ V $ 在一定范围内满足 $ \rho = \frac{m}{V} $，它的图象如图所示，则该气体的质量 $ m $ 为7 $ kg $。
]

答案： 2.7

3. 把一个长、宽、高分别为 $ 3 cm $、$ 2 cm $、$ 1 cm $ 的长方体铜块铸成一个圆柱体铜块，则该圆柱体铜块的底面积 $ S $($ cm^2 $) 与高 $ h $($ cm $) 之间的函数关系式为S=$\frac{6}{h}$。

答案： 3.S=$\frac{6}{h}$

4. 已知近视眼镜的度数 $ D $(度) 与镜片焦距 $ f $(米) 成反比例关系，且 $ 400 $ 度近视眼镜镜片的焦距为 $ 0.25 $ 米。小慧原来戴 $ 400 $ 度的近视眼镜，经过一段时间的矫正治疗后，现在只需戴镜片焦距为 $ 0.4 $ 米的眼镜了，则小慧所戴眼镜的度数降低了150度。

答案： 4.150

5. (遵义中考)反比例函数 $ y = \frac{k}{x} $($ k \neq 0 $) 与一次函数 $ y = x - 1 $ 交于点 $ A(3, n) $，则 $ k $ 的值为6。

答案： 5.6

6. (东营中考)如图，一次函数 $ y_1 = k_1x + b $ 与反比例函数 $ y_2 = \frac{k_2}{x} $ 的图象相交于 $ A $，$ B $ 两点，点 $ A $ 的横坐标为 $ 2 $，点 $ B $ 的横坐标为 $ -1 $，则不等式 $ k_1x + b ＜ \frac{k_2}{x} $ 的解集是(A)

A.$ -1 ＜ x ＜ 0 $ 或 $ x ＞ 2 $
B.$ x ＜ -1 $ 或 $ 0 ＜ x ＜ 2 $
C.$ x ＜ -1 $ 或 $ x ＞ 2 $
D.$ -1 ＜ x ＜ 2 $
]

答案： 6.A

7. （泰安中考）如图，已知一次函数 $ y = kx + b $ 的图象与反比例函数 $ y = \frac{m}{x} $ 的图象交于点 $ A(3, a) $，点 $ B(14 - 2a, 2) $。
（1）求反比例函数的表达式；
（2）若一次函数的图象与 $ y $ 轴交于点 $ C $，点 $ D $ 为点 $ C $ 关于原点 $ O $ 的对称点，求 $ \triangle ACD $ 的面积。
]

答案： 7.解：
(1)
∵点A(3,a)，点B(14-2a,2)在反比例函数上，
∴3×a=(14-2a)×2，解得a=4，则m=3×4=12.故反比例函数的表达式为y=$\frac{12}{x}$．
(2)
∵a=4，
∴A(3,4)，B(6,2).设直线AB的表达式为y=kx+b，则$\begin{cases}3k+b=4\\6k+b=2\end{cases}$，解得$\begin{cases}k=-\frac{2}{3}\\b=6\end{cases}$，
∴一次函数的表达式为y=$-\frac{2}{3}x+6$．当x=0时，y=6，
∴C(0,6).
∴OC=6.
∵点D为点C关于原点O的对称点，
∴CD=2OC=12.
∴$S_{\triangle ACD}=\frac{1}{2}CD\cdot x_A=\frac{1}{2}×12×3=18$．

8. 已知一次函数 $ y_1 = -x + 2 $，反比例函数 $ y_2 = -\frac{8}{x} $，当 $ y_1 ＜ y_2 $ 时，$ x $ 的取值范围是-2＜x＜0或x＞4。

答案： 8.-2＜x＜0或x＞4