《2025年名校课堂九年级数学全一册鲁教版五四制山东专版》

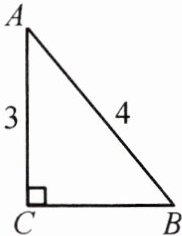
1. (柳州中考)如图，在Rt△ABC中，∠C=90°，AB=4，AC=3，则cosB=$\frac{BC}{AB}$=(C)


A.$\frac{3}{5}$
B.$\frac{4}{5}$
C.$\frac{\sqrt{7}}{4}$
D.$\frac{3}{4}$

答案： 1.C

2. (河池中考)在Rt△ABC中，∠C=90°，BC=5，AC=12，则sinB的值是(D)

A.$\frac{5}{12}$
B.$\frac{12}{5}$
C.$\frac{5}{13}$
D.$\frac{12}{13}$

答案： 2.D

3. (兰州中考)在Rt△ABC中，∠C=90°，sinA=$\frac{3}{5}$，BC=6，则AB=(D)

A.4
B.6
C.8
D.10

答案： 3.D

4. (攀枝花中考)在△ABC中，∠A，∠B，∠C的对边分别为a，b，c.已知a=6，b=8，c=10，则cosA的值为(C)

A.$\frac{3}{5}$
B.$\frac{3}{4}$
C.$\frac{4}{5}$
D.$\frac{4}{3}$

答案： 4.C

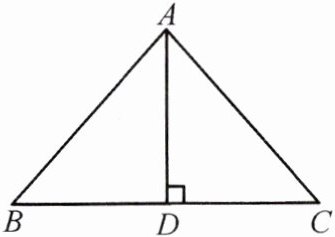
5. 如图，在△ABC中，AB=AC=6，BC=8，AD⊥BC于点D.
(1)求AD的值；
(2)求sinB，cosC的值.

答案： 5.解：
(1)
∵AB=AC,AD⊥BC,
∴$BD=CD=\frac{1}{2}BC=8×\frac{1}{2}=4.$
∴$AD=\sqrt{AB^{2}-BD^{2}}=\sqrt{6^{2}-4^{2}}=2\sqrt{5}. (2) sinB=\frac{AD}{AB}=\frac{2\sqrt{5}}{6}=\frac{\sqrt{5}}{3},cosC=\frac{CD}{AC}=\frac{4}{6}=\frac{2}{3}.$

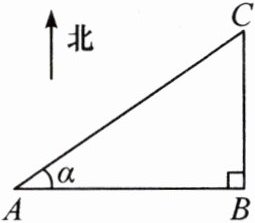
6. (南充中考)如图，小兵同学从A处出发向正东方向走x米到达B处，再向正北方向走到C处.已知∠BAC=α，则A，C两处相距(B)


A.$\frac{x}{\sin\alpha}$米
B.$\frac{x}{\cos\alpha}$米
C.$x\cdot\sin\alpha$米
D.$x\cdot\cos\alpha$米

答案： 6.B

7. (滨州中考)在△ABC中，∠C=90°.若tanA=$\frac{1}{2}$，则sinB=$\frac{2\sqrt{5}}{5}$.

答案： 7.$\frac{2\sqrt{5}}{5}$

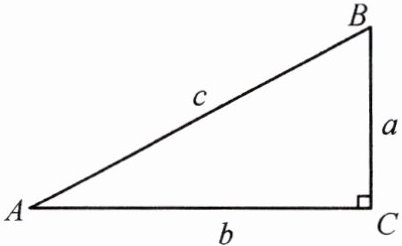
8. (教材九上P30习题T3变式与应用)如图，在Rt△ABC中，∠C=90°，a，b，c分别表示Rt△ABC中∠A，∠B，∠C的对边.
(1)求sinA，cosB；
(2)求tanA，tanB，tanA·tanB；
(3)观察(1)(2)中的计算结果，若α+β=90°，试猜想sinα与cosβ，tanα与tanβ之间有什么关系吗？
(4)应用：
①在Rt△ABC中，∠C=90°，sinA=$\frac{2}{3}$，则cosB的值为$\frac{2}{3}$；
②在Rt△ABC中，∠C=90°，tanA=2，则tanB=$\frac{1}{2}$.

答案： 8.解：
(1)在Rt△ABC中，∠C=90°,
∴$sinA=\frac{BC}{AB}=\frac{a}{c},cosB=\frac{BC}{AB}=\frac{a}{c}.(2)$在Rt△ABC中，∠C=90°,
∴$tanA=\frac{BC}{AC}=\frac{a}{b},tanB=\frac{AC}{BC}=\frac{b}{a},tanA·tanB=\frac{a}{b}·\frac{b}{a}=1.(3)$由
(1)知sinα=cosβ,由
(2)知$tanα·tanβ=1.(4)①\frac{2}{3} ②\frac{1}{2}$