《2025年名校课堂九年级数学全一册鲁教版五四制山东专版》

11. (泰安中考)在一次综合实践活动中，某学校数学兴趣小组对一电视发射塔的高度进行了测量. 如图，在塔前 $ C $ 处，测得该塔顶端 $ B $ 的仰角为 $ 50^{\circ} $，后退 $ 60 m (CD = 60 m) $ 到 $ D $ 处有一平台，在高 $ 2 m (DE = 2 m) $ 的平台上的 $ E $ 处，测得 $ B $ 的仰角为 $ 26.6^{\circ} $，则该电视发射塔的高度 $ AB $ 为55$ m $.(精确到 $ 1 m $，参考数据：$ \tan 50^{\circ} \approx 1.2 $，$ \tan 26.6^{\circ} \approx 0.5 $)

答案： 11.55

12. (东营河口区期中)如图，这是小强洗漱时的侧面示意图，洗漱台（矩形 $ ABCD $）靠墙摆放，高 $ AD = 80 cm $，宽 $ AB = 48 cm $，小强身高为 $ 166 cm $，下半身 $ FG = 100 cm $，洗漱时下半身与地面成 $ 80^{\circ} (\angle FGK = 80^{\circ}) $，身体前倾成 $ 125^{\circ} (\angle EFG = 125^{\circ}) $，脚与洗漱台的距离 $ GC = 15 cm $（点 $ D $，$ C $，$ G $ 在同一条直线上），此时小强的头部 $ E $ 与地面 $ DK $ 的距离是多少？（结果精确到 $ 0.1 cm $，参考数据：$ \cos 80^{\circ} \approx 0.17 $，$ \sin 80^{\circ} \approx 0.98 $，$ \sqrt{2} \approx 1.414 $）

答案： 12.解：过点F作FN⊥DK于点N，过点E作EM⊥FN于点M.
∵EF+FG=166cm，FG=100cm，
∴EF=166-100=66(cm).
∵∠FGK=80°，
∴FN=FG·sin80°≈100×0.98=98(cm).
∵∠EFG=125°，∠GFN=90°-∠FGK=10°，
∴∠EFM=180°-∠EFG-∠GFN=180°-125°-10°=45°.
∴$FM=EF·cos45°=66×\frac{\sqrt{2}}{2}=33\sqrt{2}≈46.66(cm).$
∴MN=
FN+FM≈144.7(cm).答：此时小强的头部E与地面DK的距离约为144.7cm.

13. 学完了三角函数知识后，某校“数学社团”的同学决定用自己学到的知识测量电视塔的高度，他们把“测量电视塔的高”作为一项课题活动，并制定了测量方案，利用课余时间完成了实地测量，测量结果如表：

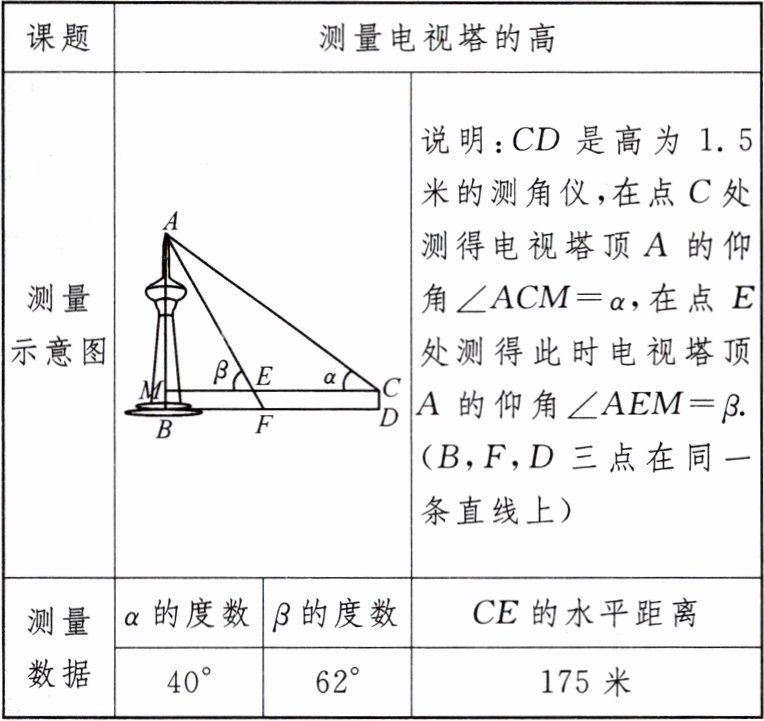
(1)请根据上表中的测量数据，求电视塔的高 $ AB $ 约为267.2米；(结果精确到 $ 0.1 $ 米，参考数据：$ \sin 40^{\circ} \approx 0.64 $，$ \cos 40^{\circ} \approx 0.77 $，$ \tan 40^{\circ} \approx 0.84 $，$ \sin 62^{\circ} \approx 0.88 $，$ \cos 62^{\circ} \approx 0.47 $，$ \tan 62^{\circ} \approx 1.88 $)
(2)“工程简介”中电视塔的高度为 $ 268 $ 米，请结合本次测量结果，提出一条减小误差的合理化建议.

答案： 13.解：
(1)267.2
(2)“工程简介”中电视塔的高度为 268 米，请结合本次测量结果，提出一条减小误差的合理化建议.