《2025年名校课堂九年级数学全一册鲁教版五四制山东专版》

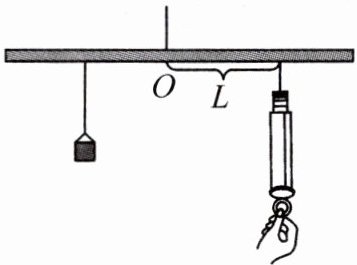
11. 如图,取一根长 $ 100 \mathrm { cm } $ 的匀质木杆,用细绳绑在木杆的中点 $ O $ 将其吊起来,在中点 $ O $ 的左侧,距离中点 $ 25 \mathrm { cm } $ 处挂一个重 $ 9.8 \mathrm { N } $ 的物体,在中点 $ O $ 右侧用一个弹簧秤向下拉,使木杆处于水平状态.如果把弹簧秤与中点 $ O $ 的距离 $ L ( \mathrm { cm } ) $ 记作 $ x $,弹簧秤的示数 $ F ( \mathrm { N } ) $ 记作 $ y $,下表中有几对数值满足 $ y $ 与 $ x $ 的函数关系式(C)


A.$ 1 $ 对
B.$ 2 $ 对
C.$ 3 $ 对
D.$ 4 $ 对

答案： 11.C

12. (淄博中考)如图,直线 $ y = k x + b $ 与双曲线 $ y = \frac { m } { x } $ 相交于点 $ A ( 2,3 ) $,$ B ( n, 1 ) $.
(1)求双曲线及直线对应的函数表达式;
(2)将直线 $ A B $ 向下平移至 $ C D $ 处,其中点 $ C ( - 2,0 ) $,点 $ D $ 在 $ y $ 轴上,连接 $ A D $,$ B D $,求 $ \triangle A B D $ 的面积;
(3)请直接写出关于 $ x $ 的不等式 $ k x + b ＞ \frac { m } { x } $ 的解集.

答案： 12.解：
(1)将A(2,3)代入$y=\frac{m}{x}，$得m=6.
∴双曲线的表达式为$y=\frac{6}{x}.$将B(n,1)代入$y=\frac{6}{x}，$得n=6.
∴B(6,1).将A(2,3),B(6,1)代入y=kx+b，得$\begin{cases}2k+b=3\\6k+b=1\end{cases},$解得$\begin{cases}k=-\frac{1}{2}\\b=4\end{cases}.$
∴直线的表达式为$y=-\frac{1}{2}x+4.(2)$
∵直线AB向下平移至CD处，
∴AB//CD.设直线CD的表达式为$y=-\frac{1}{2}x+n.$将C(-2,0)代入，得1+n=0，解得n=-1.
∴直线CD的表达式为$y=-\frac{1}{2}x-1.$当x=0时，y=-1.
∴D(0,-1).设直线AB与y轴交于点H.
∴H(0,4).
∴HD=5.
∴$S_{\triangle ABD}=S_{\triangle HBD}-S_{\triangle HAD}=\frac{1}{2}HD\cdot(x_B-x_A)=\frac{1}{2}×5×4=10.(3)2＜x＜6$或x＜0.

13. 如图,四边形 $ O A B C $ 是平行四边形,对角线 $ O B $ 在 $ y $ 轴正半轴上,位于第一象限的点 $ A $ 和第二象限的点 $ C $ 分别在双曲线 $ y = \frac { k _ { 1 } } { x } $ 和 $ y = \frac { k _ { 2 } } { x } $ 的一支上,分别过点 $ A $,$ C $ 作 $ x $ 轴的垂线,垂足分别为 $ M $ 和 $ N $,则有以下的结论:
① $ \frac { A M } { C N } = \frac { | k _ { 1 } | } { | k _ { 2 } | } $;
②阴影部分面积是 $ \frac { 1 } { 2 } ( k _ { 1 } + k _ { 2 } ) $;
③当 $ \angle A O C = 90 ^ { \circ } $ 时,$ | k _ { 1 } | = | k _ { 2 } | $;
④若 $ O A B C $ 是菱形,则两双曲线既关于 $ x $ 轴对称,也关于 $ y $ 轴对称;
⑤若 $ A C // M N $,则四边形 $ O A B C $ 的面积为 $ 2 k _ { 1 } $.
其中正确的结论是①④⑤(把所有正确的结论的序号都填上).

答案： 13.①④⑤

14. 如图,这是 $ 4 $ 个台阶的示意图,每个台阶的高和宽分别是 $ 1 $ 和 $ 2 $,每个台阶凸出的角的顶点记作 $ T _ { m } $ ($ m $ 为 $ 1 \sim 4 $ 的整数),函数 $ y = \frac { k } { x } ( x ＞ 0 ) $ 的图象为曲线 $ L $.若曲线 $ L $ 使得 $ T _ { 1 } \sim T _ { 4 } $ 这些点分布在它的两侧,每侧各 $ 2 $ 个点,则 $ k $ 的取值范围是8＜k＜12.

答案： 14.8＜k＜12