《2025年同步练习册配套检测卷七年级数学上册鲁教版五四制》

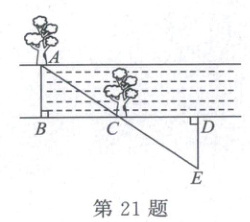
21. (10 分)如图,某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的：
① 在河流的一条岸边 $ B $ 点,选对岸正对的一棵树 $ A $；
② 沿河岸直走 20m 有一树 $ C $,继续前行 20m 到达 $ D $ 处；
③ 从 $ D $ 处沿河岸垂直的方向行走,当到达 $ A $ 树正好被 $ C $ 树遮挡住的 $ E $ 处时停止行走；
④ 测得 $ DE $ 的长为 5m.
根据他们的做法,回答下列问题：
(1)河的宽度是多少米？
(2)请你证明他们做法的正确性.

答案：
(1) 5米
(2) 证明：
∵ 两岸平行，AB为对岸正对的树，
∴ AB⊥BD，即∠ABC=90°．
∵ DE沿河岸垂直方向行走，
∴ DE⊥BD，即∠EDC=90°，
∴ ∠ABC=∠EDC．
由步骤②得BC=CD=20m，即BC=DC．
∵ A、C、E三点共线，
∴ ∠ACB=∠ECD（对顶角相等）．
在△ABC和△EDC中，
$\left\{\begin{array}{l} ∠ABC=∠EDC\\ BC=DC\\ ∠ACB=∠ECD\end{array}\right.$
∴ △ABC≌△EDC（ASA）．
∴ AB=DE．
∵ DE=5m，
∴ AB=5m，即河宽为5m．