第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
24. (16 分)三角形内角的一条边与另一条边的反向延长线组成的角,称为三角形的外角.已知三角形的一个外角等于与它不相邻的两个内角的和,那么三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
尝试探究:
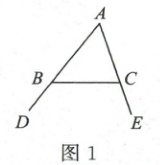
如图 1,∠DBC 与∠ECB 分别为△ABC 的两个外角,那么∠A 与∠DBC + ∠ECB 之间存在怎样的数量关系?为什么?
初步应用:
(1)如图 2,在三角形纸片 ABC 中剪去△CED,得到四边形 ABDE,已知∠1 = 130°,则∠2 - ∠C = ______.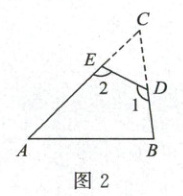
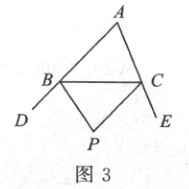
(2)如图 3,在△ABC 中,已知 BP,CP 分别平分外角∠DBC 和∠ECB,请问:∠P 与∠A 有何数量关系?请利用上面的结论直接写出答案.
拓展提升:
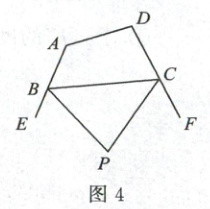
如图 4,在四边形 ABCD 中,BP,CP 分别平分∠EBC,∠FCB,请问:∠P 与∠A,∠D 有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)
尝试探究:
∠DBC + ∠ECB = ∠A + 180°。
理由:
∵∠DBC是△ABC的外角,∴∠DBC = ∠A + ∠ACB。
∵∠ECB是△ABC的外角,∴∠ECB = ∠A + ∠ABC。
∴∠DBC + ∠ECB = (∠A + ∠ACB) + (∠A + ∠ABC) = 2∠A + (∠ABC + ∠ACB)。
∵在△ABC中,∠ABC + ∠ACB = 180° - ∠A,
∴∠DBC + ∠ECB = 2∠A + (180° - ∠A) = ∠A + 180°。
初步应用:
(1)
(2)
拓展提升:
∠P = 180° - 1/2(∠A + ∠D)。
理由:
∵∠EBC是∠ABC的外角,∴∠EBC = 180° - ∠ABC。
∵∠FCB是∠BCD的外角,∴∠FCB = 180° - ∠BCD。
∴∠EBC + ∠FCB = (180° - ∠ABC) + (180° - ∠BCD) = 360° - (∠ABC + ∠BCD)。
∵四边形ABCD内角和为360°,∴∠ABC + ∠BCD = 360° - (∠A + ∠D)。
∴∠EBC + ∠FCB = 360° - [360° - (∠A + ∠D)] = ∠A + ∠D。
∵BP平分∠EBC,CP平分∠FCB,∴∠PBC = 1/2∠EBC,∠PCB = 1/2∠FCB。
在△PBC中,∠P = 180° - (∠PBC + ∠PCB) = 180° - 1/2(∠EBC + ∠FCB) = 180° - 1/2(∠A + ∠D)。
尝试探究:
如图 1,∠DBC 与∠ECB 分别为△ABC 的两个外角,那么∠A 与∠DBC + ∠ECB 之间存在怎样的数量关系?为什么?

初步应用:
(1)如图 2,在三角形纸片 ABC 中剪去△CED,得到四边形 ABDE,已知∠1 = 130°,则∠2 - ∠C = ______.

(2)如图 3,在△ABC 中,已知 BP,CP 分别平分外角∠DBC 和∠ECB,请问:∠P 与∠A 有何数量关系?请利用上面的结论直接写出答案.

拓展提升:
如图 4,在四边形 ABCD 中,BP,CP 分别平分∠EBC,∠FCB,请问:∠P 与∠A,∠D 有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)

尝试探究:
∠DBC + ∠ECB = ∠A + 180°。
理由:
∵∠DBC是△ABC的外角,∴∠DBC = ∠A + ∠ACB。
∵∠ECB是△ABC的外角,∴∠ECB = ∠A + ∠ABC。
∴∠DBC + ∠ECB = (∠A + ∠ACB) + (∠A + ∠ABC) = 2∠A + (∠ABC + ∠ACB)。
∵在△ABC中,∠ABC + ∠ACB = 180° - ∠A,
∴∠DBC + ∠ECB = 2∠A + (180° - ∠A) = ∠A + 180°。
初步应用:
(1)
50°
(2)
∠P = 90° - 1/2∠A
拓展提升:
∠P = 180° - 1/2(∠A + ∠D)。
理由:
∵∠EBC是∠ABC的外角,∴∠EBC = 180° - ∠ABC。
∵∠FCB是∠BCD的外角,∴∠FCB = 180° - ∠BCD。
∴∠EBC + ∠FCB = (180° - ∠ABC) + (180° - ∠BCD) = 360° - (∠ABC + ∠BCD)。
∵四边形ABCD内角和为360°,∴∠ABC + ∠BCD = 360° - (∠A + ∠D)。
∴∠EBC + ∠FCB = 360° - [360° - (∠A + ∠D)] = ∠A + ∠D。
∵BP平分∠EBC,CP平分∠FCB,∴∠PBC = 1/2∠EBC,∠PCB = 1/2∠FCB。
在△PBC中,∠P = 180° - (∠PBC + ∠PCB) = 180° - 1/2(∠EBC + ∠FCB) = 180° - 1/2(∠A + ∠D)。
答案:
尝试探究:
∠DBC + ∠ECB = ∠A + 180°。
理由:
∵∠DBC是△ABC的外角,
∴∠DBC = ∠A + ∠ACB。
∵∠ECB是△ABC的外角,
∴∠ECB = ∠A + ∠ABC。
∴∠DBC + ∠ECB = (∠A + ∠ACB) + (∠A + ∠ABC) = 2∠A + (∠ABC + ∠ACB)。
∵在△ABC中,∠ABC + ∠ACB = 180° - ∠A,
∴∠DBC + ∠ECB = 2∠A + (180° - ∠A) = ∠A + 180°。
初步应用:
(1)50°。
(2)∠P = 90° - 1/2∠A。
拓展提升:
∠P = 180° - 1/2(∠A + ∠D)。
理由:
∵∠EBC是∠ABC的外角,
∴∠EBC = 180° - ∠ABC。
∵∠FCB是∠BCD的外角,
∴∠FCB = 180° - ∠BCD。
∴∠EBC + ∠FCB = (180° - ∠ABC) + (180° - ∠BCD) = 360° - (∠ABC + ∠BCD)。
∵四边形ABCD内角和为360°,
∴∠ABC + ∠BCD = 360° - (∠A + ∠D)。
∴∠EBC + ∠FCB = 360° - [360° - (∠A + ∠D)] = ∠A + ∠D。
∵BP平分∠EBC,CP平分∠FCB,
∴∠PBC = 1/2∠EBC,∠PCB = 1/2∠FCB。
在△PBC中,∠P = 180° - (∠PBC + ∠PCB) = 180° - 1/2(∠EBC + ∠FCB) = 180° - 1/2(∠A + ∠D)。
∠DBC + ∠ECB = ∠A + 180°。
理由:
∵∠DBC是△ABC的外角,
∴∠DBC = ∠A + ∠ACB。
∵∠ECB是△ABC的外角,
∴∠ECB = ∠A + ∠ABC。
∴∠DBC + ∠ECB = (∠A + ∠ACB) + (∠A + ∠ABC) = 2∠A + (∠ABC + ∠ACB)。
∵在△ABC中,∠ABC + ∠ACB = 180° - ∠A,
∴∠DBC + ∠ECB = 2∠A + (180° - ∠A) = ∠A + 180°。
初步应用:
(1)50°。
(2)∠P = 90° - 1/2∠A。
拓展提升:
∠P = 180° - 1/2(∠A + ∠D)。
理由:
∵∠EBC是∠ABC的外角,
∴∠EBC = 180° - ∠ABC。
∵∠FCB是∠BCD的外角,
∴∠FCB = 180° - ∠BCD。
∴∠EBC + ∠FCB = (180° - ∠ABC) + (180° - ∠BCD) = 360° - (∠ABC + ∠BCD)。
∵四边形ABCD内角和为360°,
∴∠ABC + ∠BCD = 360° - (∠A + ∠D)。
∴∠EBC + ∠FCB = 360° - [360° - (∠A + ∠D)] = ∠A + ∠D。
∵BP平分∠EBC,CP平分∠FCB,
∴∠PBC = 1/2∠EBC,∠PCB = 1/2∠FCB。
在△PBC中,∠P = 180° - (∠PBC + ∠PCB) = 180° - 1/2(∠EBC + ∠FCB) = 180° - 1/2(∠A + ∠D)。
查看更多完整答案,请扫码查看


