《2025年同步练习册配套检测卷七年级数学上册鲁教版五四制》

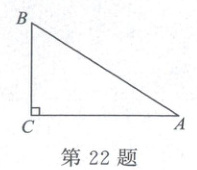
22. (10 分)如图,在 $\triangle ABC$ 中,$\angle C = 90^{\circ}$,$AB = 10$ cm,$BC = 6$ cm. 若动点 $P$ 从点 $C$ 出发,沿线段 $CA$ 向点 $A$ 运动,到达 $A$ 点后停止运动,且速度为每秒 2 cm,设出发的时间为 $t$ s.
(1)当 $t$ 为何值时,$\triangle PBC$ 是等腰三角形？
(2)过点 $P$ 作 $PH\perp AB$,垂足为点 $H$,当 $H$ 为 $AB$ 的中点时,求 $t$ 的值.

答案：
(1) 在Rt△ABC中，∠C=90°，AB=10cm，BC=6cm，由勾股定理得AC=√(AB²-BC²)=√(10²-6²)=8cm。
△PBC为等腰三角形，∠C=90°，分情况讨论：
① PC=BC：PC=2t，BC=6，
∴2t=6，t=3。
② PB=BC：PB=BC=6，在Rt△PBC中，PC²+BC²=PB²，即PC²+6²=6²，PC=0，t=0（P与C重合，不构成三角形，舍去）。
③ PB=PC：在Rt△PBC中，PC²+BC²=PB²，PB=PC时BC=0，不可能。
综上，t=3。
(2) H为AB中点，AB=10，
∴AH=HB=5cm。设PH=h，PC=2t，PA=8-2t。
在Rt△APH中，PH²+AH²=PA²，即h²+5²=(8-2t)²①。
在Rt△PBC中，PB²=PC²+BC²=(2t)²+6²②。
在Rt△PBH中，PB²=PH²+HB²=h²+5²③。
由②③得h²+25=4t²+36，h²=4t²+11④。
将④代入①：4t²+11+25=(8-2t)²，化简得32t=28，t=7/8。
(1) t=3；
(2) t=7/8。

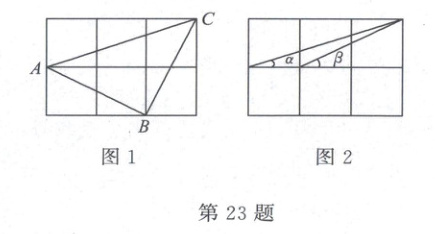
23. (10 分)在六个边长为 1 的小正方形组成的网格中,
(1)如图 1,$A$,$B$,$C$ 是三个格点(即小正方形的顶点),判断 $\triangle ABC$ 的形状,并说明理由；
(2)如图 2,连接三格和两格的对角线,求 $\angle \alpha$ 和 $\angle \beta$ 的度数之和.

答案：
(1) $AB = \sqrt{1^{2} + 2^{2}}=\sqrt{5}$；$BC = \sqrt{1^{2} + 2^{2}}=\sqrt{5}$；$AC = \sqrt{1^{2} + 3^{2}}=\sqrt{10}$。
因为$AB^{2}+BC^{2}=5 + 5 = 10$，$AC^{2}=10$，所以$AB^{2}+BC^{2}=AC^{2}$，且$AB = BC$。
故$\triangle ABC$是等腰直角三角形。
(2) 连接$DE$、$EF$（设小正方形网格中，$D$在$\angle \alpha$顶点左下方格点，$E$在$\angle \alpha$顶点，$F$在$\angle \beta$顶点）。
$DE = \sqrt{1^{2} + 1^{2}}=\sqrt{2}$，$EF = \sqrt{1^{2} + 1^{2}}=\sqrt{2}$，$DF = 2$。
因为$DE^{2}+EF^{2}=2 + 2 = 4$，$DF^{2}=4$，所以$\triangle DEF$是等腰直角三角形，$\angle DEF = 90^{\circ}$。
所以$\angle \alpha+\angle \beta = 45^{\circ}+45^{\circ}=45^{\circ}$（或由$\angle \alpha=\angle EDF = 45^{\circ}$，$\angle \beta=\angle EFD = 45^{\circ}$，得$\angle \alpha+\angle \beta = 45^{\circ}$ ）。
综上，答案为：
(1)等腰直角三角形，理由如上述；
(2)$45^{\circ}$。