《2025年作业本浙江教育出版社八年级数学上册浙教版》

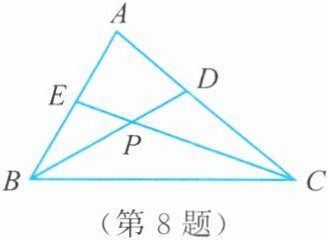
8. 如图,在$\triangle ABC$中,$\angle ABC$,$\angle ACB的平分线BD$,$CE交于点P$。
(1) 若$\angle ABC = 60^{\circ}$,$\angle ACB = 40^{\circ}$,求$\angle BPC$的度数。
(2) 若$\angle A = 80^{\circ}$,求$\angle BPC$的度数。
(3) 若$\angle A = x^{\circ}$,用含$x的代数式表示\angle BPC$的度数。

答案： （1）因为∠ABC=60°，∠ACB=40°，BD，CE分别平分∠ABC，∠ACB，所以∠PBC=30°，∠PCB=20°，所以∠BPC=180°-(∠PBC+∠PCB)=130°。
（2）因为∠A=80°，所以∠ABC+∠ACB=100°。BD，CE分别平分∠ABC，∠ACB，所以∠PBC+∠PCB= $\frac{1}{2}$∠ABC+ $\frac{1}{2}$∠ACB=50°，所以∠BPC=180°-(∠PBC+∠PCB)=130°。
（3）因为∠A=x°，所以∠ABC+∠ACB=(180-x)°。因为BD，CE分别平分∠ABC，∠ACB，所以∠PBC+∠PCB= $\frac{1}{2}$(∠ABC+∠ACB)= $\frac{1}{2}$(180-x)°，所以∠BPC=180°-(∠PBC+∠PCB)=180°- $\frac{1}{2}$(180-x)°= $(90+\frac{1}{2}x)$°。

9. 在$\triangle ABC$中,$AD$,$AE分别是BC$边上的中线与高线,设$k = DE:BD$。
(1) 若$k ＞ 1$,则$\triangle ABC$一定是钝角三角形(在“钝角”“直角”或“锐角”中选择)。
(2) 小明认为：若$k ＜ 1$,则$\triangle ABC$一定是锐角三角形。你赞同小明的观点吗？请阐述你的理由。
不赞同。理由：若k＜1，可得∠C和∠B是锐角。但∠A可能是直角，也可能是钝角，因此这个三角形不一定是锐角三角形。

答案： （1）钝角
（2）不赞同。理由：若k＜1，可得∠C和∠B是锐角。但∠A可能是直角，也可能是钝角，因此这个三角形不一定是锐角三角形。