《2025年作业本浙江教育出版社八年级数学上册浙教版》

9. 如图,在$\triangle ABC$中,$AB = AC$,$\angle BAC= \alpha$。点$A在直线m$上,在直线$m上另取两个互不重合的点D$,$E$,且满足$\angle BDA= \angle AEC= \angle BAC$。

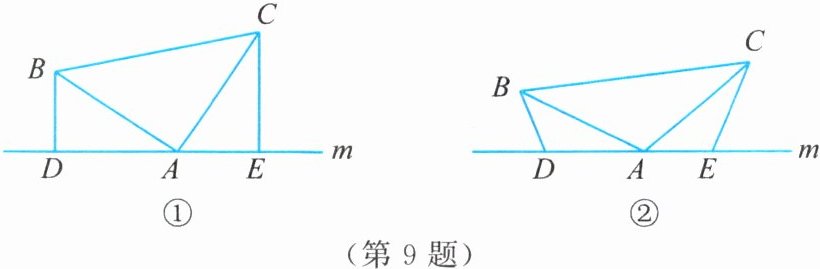
(1)如图①,当$\alpha = 90^{\circ}$时,猜想$DE$,$BD$,$CE$之间的数量关系：DE=BD+CE(直接写出结论)。
(2)如图②,当$0^{\circ}\lt\alpha\lt180^{\circ}$时,问题(1)中的结论还成立吗？若成立,给出证明过程；若不成立,请说明理由。
(1)中的结论还成立。理由如下:因为∠BDA=∠BAC=∠AEC=α,所以∠BAD+∠EAC=∠BAD+∠DBA=180°−α,所以∠DBA=∠EAC。又因为AB=AC,所以△DBA≌△EAC(AAS)。所以BD=AE,AD=CE。所以DE=AD+AE=BD+CE。

答案：
(1)DE=BD+CE
(2)
(1)中的结论还成立。理由如下:因为∠BDA=∠BAC=∠AEC=α,所以∠BAD+∠EAC=∠BAD+∠DBA=180°−α,所以∠DBA=∠EAC。又因为AB=AC,所以△DBA≌△EAC(AAS)。所以BD=AE,AD=CE。所以DE=AD+AE=BD+CE。