《2025年作业本浙江教育出版社八年级数学上册浙教版》

1. 自行车的车架采用了三角形结构,这样设计的依据是三角形具有稳定性。

答案： 稳定性

2. 用刻度尺和圆规画一个三角形,使它的三边长分别是 2 cm,3 cm,4 cm。(只要求画出图形,保留画图痕迹,不必写画法)

答案： 答题卡：
1. 画一条线段$AB = 4 cm$（用刻度尺）。
2. 以点$A$为圆心，$3 cm$为半径画弧（用圆规）。
3. 以点$B$为圆心，$2 cm$为半径画弧，两弧交点记为$C$。
4. 连接$AC$和$BC$。
则$\triangle ABC$为所求作的三角形。
（图略，需保留画图时线段、弧的痕迹）。

3. 已知：如图,$AB = AC$,$DB = DC$。求证：$\triangle ABD≌\triangle ACD$。请完成下面的推理过程(填空)。
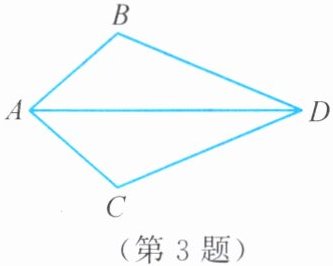
证明：在$\triangle ABD和\triangle ACD$中,
$\left\{ \begin{array}{l} AB = AC(已知), \\ DB = DC(已知), \\ AD = AD(公共边), \end{array} \right.$
所以$\triangle ABD≌\triangle ACD$(SSS)。

答案： AC;已知;AD;SSS

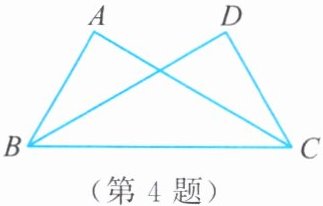
4. 已知：如图,$AB = DC$,$AC = DB$。求证：
(1)$\triangle ABC≌\triangle DCB$；
(2)$\angle ABD = \angle DCA$。

答案： （1）由AB=DC，AC=DB，BC=CB，可证△ABC≌△DCB(SSS)。（2）因为△ABC≌△DCB，所以∠ACB=∠DBC，∠ABC=∠DCB，所以∠ABC - ∠DBC=∠DCB - ∠ACB，即∠ABD=∠DCA。