第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
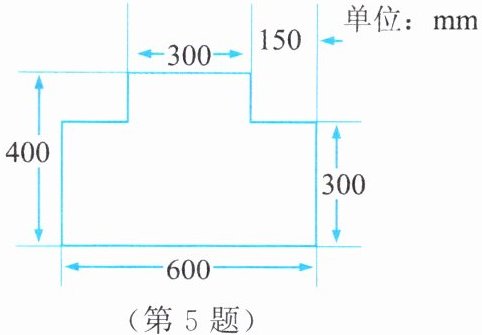
5. 一个机械零件的横截面如图所示。请完成以下任务。
(1) 选择合适的比例,建立适当的直角坐标系,并在直角坐标系中作出这个零件的横截面。
(2) 写出轮廓线各个转折点的坐标。
(1) 选择合适的比例,建立适当的直角坐标系,并在直角坐标系中作出这个零件的横截面。
(2) 写出轮廓线各个转折点的坐标。

答案:
1. (1)
选择$1:100$的比例(比例可根据实际情况选择,这里仅为示例),以图形的左下角顶点为原点$(0,0)$,水平向右为$x$轴正方向,竖直向上为$y$轴正方向建立直角坐标系。
根据比例,实际长度$l$与图上长度$l'$的关系为$l'=\frac{l}{100}$(单位:$cm$,因为$1mm = 0.1cm$)。
例如:实际长度$600mm = 60cm$,图上长度$x = 60÷100 = 0.6cm$;实际长度$400mm = 40cm$,图上长度$y = 40÷100 = 0.4cm$等,然后按照图形形状作出横截面。
2. (2)
设原点为$O(0,0)$。
从左到右,从下到上:
第一个转折点:设最左边底部点为$A(0,0)$;
第二个转折点:水平向右$600mm$,则$B(600,0)$(单位:$mm$);
第三个转折点:从$B$点竖直向上$300mm$,则$C(600,300)$;
第四个转折点:从$C$点向左$150mm$,则$D(600 - 150,300)=(450,300)$;
第五个转折点:从$D$点向上到与左边高度相同,因为左边总高度$400mm$,所以$E(450,400)$;
第六个转折点:从$E$点向左$300mm$,则$F(450-300,400)=(150,400)$;
第七个转折点:从$F$点向下到与左边底部连接,即$G(150,0)$(这里$G$与$A$重合于实际图形的连接点)。
所以轮廓线各个转折点的坐标(单位:$mm$)为$(0,0)$,$(600,0)$,$(600,300)$,$(450,300)$,$(450,400)$,$(150,400)$。
选择$1:100$的比例(比例可根据实际情况选择,这里仅为示例),以图形的左下角顶点为原点$(0,0)$,水平向右为$x$轴正方向,竖直向上为$y$轴正方向建立直角坐标系。
根据比例,实际长度$l$与图上长度$l'$的关系为$l'=\frac{l}{100}$(单位:$cm$,因为$1mm = 0.1cm$)。
例如:实际长度$600mm = 60cm$,图上长度$x = 60÷100 = 0.6cm$;实际长度$400mm = 40cm$,图上长度$y = 40÷100 = 0.4cm$等,然后按照图形形状作出横截面。
2. (2)
设原点为$O(0,0)$。
从左到右,从下到上:
第一个转折点:设最左边底部点为$A(0,0)$;
第二个转折点:水平向右$600mm$,则$B(600,0)$(单位:$mm$);
第三个转折点:从$B$点竖直向上$300mm$,则$C(600,300)$;
第四个转折点:从$C$点向左$150mm$,则$D(600 - 150,300)=(450,300)$;
第五个转折点:从$D$点向上到与左边高度相同,因为左边总高度$400mm$,所以$E(450,400)$;
第六个转折点:从$E$点向左$300mm$,则$F(450-300,400)=(150,400)$;
第七个转折点:从$F$点向下到与左边底部连接,即$G(150,0)$(这里$G$与$A$重合于实际图形的连接点)。
所以轮廓线各个转折点的坐标(单位:$mm$)为$(0,0)$,$(600,0)$,$(600,300)$,$(450,300)$,$(450,400)$,$(150,400)$。
6. 如图,四盏灯笼的位置 $ A,B,C,D $ 的坐标分别是 $ (-1,b),(1,b),(2,b),(3.5,b) $。平移 $ y $ 轴右侧的一盏灯笼,使得两侧的灯笼关于 $ y $ 轴对称,则平移的方法可以是(
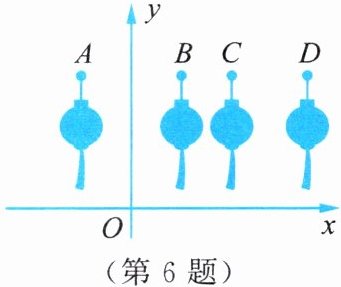
A.将 $ B $ 向左平移 $ 4.5 $ 个单位
B.将 $ C $ 向左平移 $ 4 $ 个单位
C.将 $ D $ 向左平移 $ 5.5 $ 个单位
D.将 $ C $ 向左平移 $ 3.5 $ 个单位
C
)。
A.将 $ B $ 向左平移 $ 4.5 $ 个单位
B.将 $ C $ 向左平移 $ 4 $ 个单位
C.将 $ D $ 向左平移 $ 5.5 $ 个单位
D.将 $ C $ 向左平移 $ 3.5 $ 个单位
答案:
C
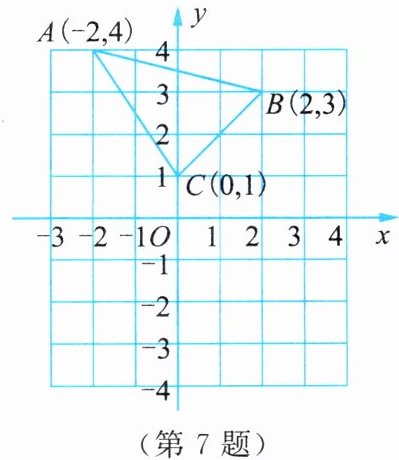
7. 如图,已知 $ \triangle ABC $ 在直角坐标系中,将 $ \triangle ABC $ 各顶点的纵坐标分别乘 $ -1 $,横坐标不变,得点 $ A',B',C' $。
(1) 写出点 $ A',B',C' $ 的坐标。
(2) 作 $ \triangle A'B'C' $。
(3) $ \triangle A'B'C' $ 与 $ \triangle ABC $ 有什么关系?
(1) 写出点 $ A',B',C' $ 的坐标。
(2) 作 $ \triangle A'B'C' $。
(3) $ \triangle A'B'C' $ 与 $ \triangle ABC $ 有什么关系?

答案:
(1) A'(-2,-4),B'(2,-3),C'(0,-1)
(2) 略
(3) △A'B'C'与△ABC关于x轴对称
(1) A'(-2,-4),B'(2,-3),C'(0,-1)
(2) 略
(3) △A'B'C'与△ABC关于x轴对称
查看更多完整答案,请扫码查看


