《2025年作业本浙江教育出版社八年级数学上册浙教版》

1. 在等腰三角形 $ ABC $ 中,$ AB = AC $。
(1) 若 $ \angle A = 60° $,则 $ \angle B $ 的度数是60°,$ \angle C $ 的度数是60°；
(2) 若 $ \angle B = 35° $,则 $ \angle A $ 的度数是110°,$ \angle C $ 的度数是35°。

答案： （1）60°；60° （2）110°；35°

2. 如图,已知点 $ D $,$ E $ 是 $ BC $ 上的三等分点,$ \triangle ADE $ 是等边三角形,则 $ \angle BAC $ 的度数为120°。

答案： 120°

3. 等腰三角形顶角的度数比一个底角度数的 $ 2 $ 倍多 $ 20° $,则这个底角的度数是(B)。
A.$ 30° $
B.$ 40° $
C.$ 50° $
D.$ 60° $

答案： B

4. 如图,房屋的顶角 $ \angle BAC = 100° $,过屋顶 $ A $ 的立柱 $ AD \perp BC $,屋檐 $ AB = AC $。求 $ \angle B $,$ \angle C $,$ \angle BAD $,$ \angle CAD $ 的度数。

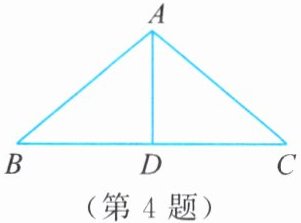
答案： ∠B=40°,∠C=40°,∠BAD=50°,∠CAD=50°。

5. 求证：等腰三角形底边上的中点到两腰的距离相等。

答案： 可依据“AAS”定理证明两底角所在的两个三角形全等。

6. 已知 $ \triangle ABC $ 的一个外角是 $ 140° $,且 $ AC = BC $。求 $ \angle C $ 的度数。

答案： 40°或100°