《2025年作业本浙江教育出版社八年级数学上册浙教版》

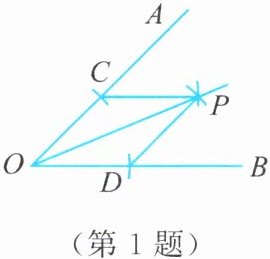
1. 如图,用直尺和圆规作$\angle AOB$的平分线,方法如下：
①以$O$为圆心,适当长为半径作弧,分别交$OA$,$OB于点C$,$D$；
②再分别以点$C$,$D$为圆心,以大于$\frac{1}{2}CD$长为半径作弧,两弧交于点$P$；
③作射线$OP$,$OP即为\angle AOB$的平分线。
由作法得$\triangle OCP\cong\triangle ODP$的依据是(D)。

A.$SAS$
B.$ASA$
C.$AAS$
D.$SSS$

答案： D

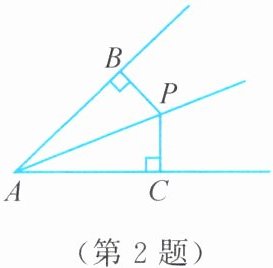
2. 如图,$AP平分\angle BAC$,$PB\perp AB于点B$,$PC\perp AC于点C$,则图中长度相等的线段是AB=AC,BP=CP。

答案： AB=AC,BP=CP

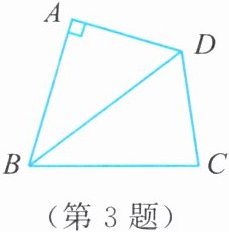
3. 如图,$BD是\angle ABC$的平分线,$DA\perp BA于点A$,$AD = 4$,$BC= 6$,则$\triangle BCD$的面积为(D)。

A.$10$
B.$24$
C.$15$
D.$12$

答案： D

4. 如图,$OD平分\angle AOB$,$DE\perp OA于点E$,$DE = 4$,$F是射线OB$上任意一点,则$DF$的长度不可能是(A)。

A.$3.9$
B.$4$
C.$4.7$
D.$5$

答案： A