《2025年作业本浙江教育出版社八年级数学上册浙教版》

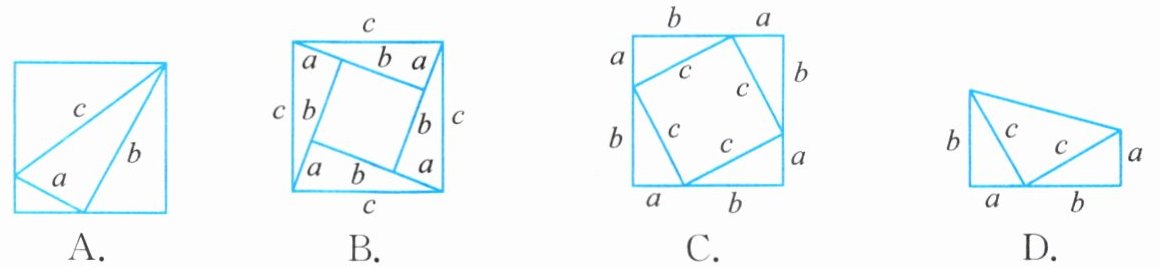
6. (多选题)若$a$,$b$为直角三角形的两直角边,$c$为斜边,下列各图能证明勾股定理的是(BCD)。

答案： BCD

7. 如图,在$\triangle ABC$中,$AD是BC$边上的高线。若$AB = 15$,$AC = 13$,$BC = 14$,求$AD$的长。

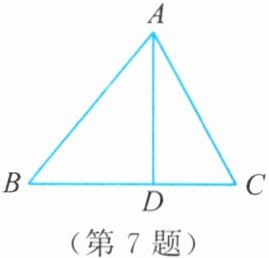
答案： 因为$AD\perp BC$，所以$AD^{2}=AB^{2}-BD^{2}=AC^{2}-CD^{2}$。设$BD=x$，则$CD=14-x$，所以$15^{2}-x^{2}=13^{2}-(14-x)^{2}$，解得$x=9$。所以$AD$的长为12。

8. 如图,将一个直立的火柴盒在桌面上横向倒下,火柴盒的一个侧面$ABCD横倒后的位置为AB'C'D'$,连结$CC'$。设$AB = a$,$BC = b$,$AC = c$,利用梯形$BCC'D'面积的不同算法可以说明勾股定理a^{2}+b^{2}= c^{2}$成立。请你尝试推导出勾股定理。

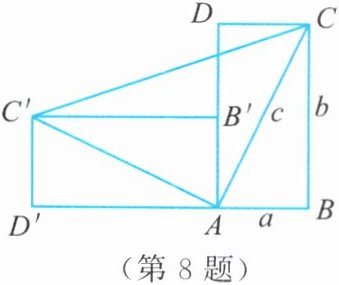
答案： 由题意可得$\frac{1}{2}(a+b)^{2}=ab+\frac{1}{2}c^{2}$，所以$(a+b)^{2}=2ab+c^{2}$，所以$a^{2}+2ab+b^{2}=2ab+c^{2}$，从而$a^{2}+b^{2}=c^{2}$。