《2025年作业本浙江教育出版社八年级数学上册浙教版》

1. 在$\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle A$,$\angle B$,$\angle C的对边分别是a$,$b$,$c$。
(1) 若$a = 3$,$b = 4$,则$c = $5。
(2) 若$a = 5$,$c = 13$,则$b = $12。
(3) 若$b = 2$,$c = 3$,则$a = $$\sqrt{5}$。

答案： （1）5 （2）12 （3）$\sqrt{5}$

2. 如图,已知两个正方形的面积分别为$64和289$,则正方形$A$的面积为225。

答案： 225

3. 利用圆规,在如图数轴上表示$-\sqrt{5}$,$\sqrt{8}$,$\sqrt{13}$的点。

答案： 1. 表示$\sqrt{5}$：在网格中取点$(1,2)$，连接原点与该点，斜边长为$\sqrt{1^2+2^2}=\sqrt{5}$。以原点为圆心，此斜边长为半径画弧，交数轴正半轴得$\sqrt{5}$，交负半轴得$-\sqrt{5}$。
2. 表示$\sqrt{8}$：在网格中取点$(2,2)$，连接原点与该点，斜边长为$\sqrt{2^2+2^2}=\sqrt{8}$。以原点为圆心，此斜边长为半径画弧，交数轴正半轴得$\sqrt{8}$。
3. 表示$\sqrt{13}$：在网格中取点$(2,3)$，连接原点与该点，斜边长为$\sqrt{2^2+3^2}=\sqrt{13}$。以原点为圆心，此斜边长为半径画弧，交数轴正半轴得$\sqrt{13}$。

4. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = 6$,$BC = 8$。$M是AB$的中点,则$CM = $5。

答案： 5

5. 如图,在$\triangle ABC$中,$AD\perp BC于点D$。若$AB = AC = 2cm$,$AD = \sqrt{2}cm$,求$BC$的长。

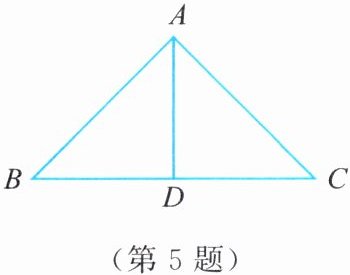
答案： 因为$AD\perp BC$，$AB=2$，$AD=\sqrt{2}$，所以$BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{2}\,cm$。又因为$AB=AC$，所以$BC=2BD=2\sqrt{2}\,cm$。