《2025年云南省标准教辅同步指导训练与检测五年级数学上册人教版》

1. 一个长方形花园长42m,宽30m,现在要在花园四周种树,四个角上都要种,每相邻两棵树之间间隔6m,一共要种(24)棵树。

答案： 解析：本题可根据在封闭线路上的植树问题的特点来求解，即在封闭线路上的植树问题，其数量与间隔数相等。
首先，可先求出长方形花园的周长，再根据间隔距离求出间隔数，进而得到种树的数量。
长方形周长公式为$C=(a + b)×2$（其中$C$表示周长，$a$表示长，$b$表示宽）。
已知长方形花园长$42m$，宽$30m$，则其周长为$(42 + 30)×2 = 144m$。
每相邻两棵树之间间隔$6m$，则间隔数为$144÷6 = 24$（个）。
因为在封闭线路上种树，树的棵数与间隔数相等，所以一共要种$24$棵树。
答案：24

2. 广场上的大钟4时敲4下,6秒敲完,12时敲12下,需要(22)秒。

答案： 4时敲4下，间隔数：4-1=3（个）
每个间隔时间：6÷3=2（秒）
12时敲12下，间隔数：12-1=11（个）
总时间：11×2=22（秒）
22

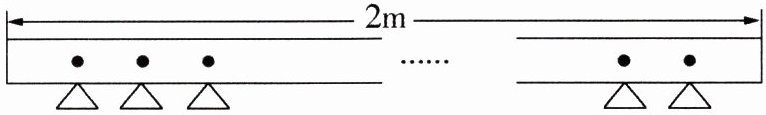
3. 下图是小聪家的晾衣架示意图,每两个衣架孔间隔10cm,这个晾衣架最多有(21)个衣架孔。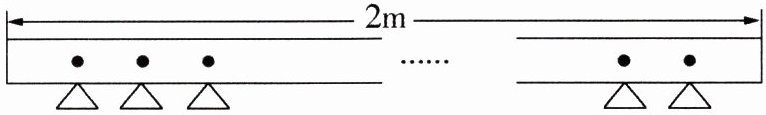

答案： 解析：本题可先将晾衣架的长度单位换算为厘米，再计算间隔数，最后根据两端都植树问题的公式求出衣架孔的数量。
先将晾衣架的长度$2m$换算为$200cm$。
计算间隔数：已知每两个衣架孔间隔$10cm$，根据“间隔数$=$总距离$÷$间隔长度”，可得间隔数为$200÷10 = 20$（个）。
计算衣架孔数量：因为晾衣架两端都有衣架孔，属于两端都植树问题，其数量与间隔数的关系为“棵数$=$间隔数$ + 1$”，所以衣架孔的数量为$20 + 1 = 21$（个）。
答案：21。

一座桥全长1800m,在桥面的两侧每隔45m安装一盏路灯(两端都安装路灯)。从桥的一端到另一端共安装(82)盏路灯。

答案： 解析：本题考查了植树问题，知识点是：盏数$=$间隔数$+ 1$，间隔数$=$总距离$÷$间距。
先求出$1800$米里面有几个$45$米，即有几个间隔，因为两端都要安装，所以盏数$=$间隔数$+ 1$，由此求出一侧安装路灯的盏数，再乘$2$求出两侧共安装路灯的盏数。
答案：$1800÷45 + 1$
$= 40 + 1$
$= 41$（盏）
$41× 2 = 82$（盏）
故答案为：$82$。

5. 新能源电动车能有效减少空气污染,幸福小区为了解决居民电动车充电问题,准备新增A、B两排充电区。A排充电区在长60m的马路一边每隔1.5m设置一个充电桩(两端都装),A排充电区一共设置了(41)个充电桩。B排充电区在车棚内侧的一边设置(两端都不装),也是每隔1.5m设置一个充电桩,一共设置了21个充电桩,车棚的长度是(33)m。

答案： 解析：本题考查了植树问题，知识点是：间隔数=棵数-1（两端都不栽），植树的棵数=间隔数+1(两端都栽)，总距离=间隔数×间距。
对于A排充电区：
已知A排充电区在长$60m$的马路一边每隔$1.5m$设置一个充电桩(两端都装)。
那么间隔数为：$60÷1.5=40(个)$。
由于两端都装，所以充电桩的数量为：$40+1=41(个)$。
对于B排充电区：
已知B排充电区在车棚内侧的一边设置(两端都不装)，一共设置了$21$个充电桩，间隔距离为$1.5m$。
由于两端都不装，所以间隔数为：$21+1=22(个)$。
那么车棚的长度为：$22×1.5=33(m)$。
答案：$41$；$33$。