《2025年暑假综合练习河北人民出版社八年级数学》

3. 先化简,再求值：$(\frac{1}{a - 2}-\frac{1}{a + 2})÷\frac{2}{2 - a}$,其中$a= \sqrt{3}-1$.

答案： 解：原式$=-\frac{2}{a+2}$.当$a=\sqrt{3}-1$时，原式$=-\frac{2}{\sqrt{3}-1+2}=1-\sqrt{3}$.

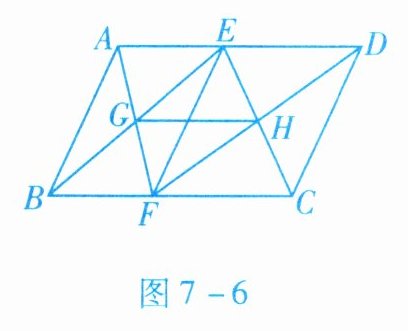
4. 如图7-6所示,在$□ ABCD$中,$EF// AB$. 求证：$GH// BC$,$GH= \frac{1}{2}BC$.

答案： 证明：在$□ ABCD$中，$AB// CD$，$AD// BC$. 又$\because EF// AB$，$\therefore$四边形$ABFE$和四边形$EFCD$都是平行四边形.$\because G$，$H$分别是这两个平行四边形对角线的交点，$\therefore G$是$BE$的中点，$H$是$CE$的中点. $\therefore GH// BC$，$GH=\frac{1}{2}BC$.

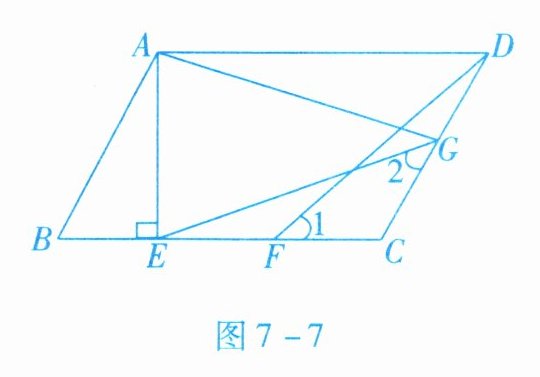
5. 如图7-7所示,在$□ ABCD$中,$AE\perp BC$,垂足为E,$CE= CD$,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,$\angle 1= \angle 2$.
(1) 若$CF= 2$,$AE= 3$,求BE的长；
(2) 求证：$CD= 2CG$.

答案： （1）解：$\because CE=CD$，点$F$为$CE$的中点，$CF=2$，$\therefore DC=CE=2CF=4$.$\because$四边形$ABCD$是平行四边形，$\therefore AB=CD=4$.$\because AE\perp BC$，$\therefore \angle AEB=90^{\circ}$.在$Rt\triangle ABE$中，由勾股定理得：$BE=\sqrt{4^{2}-3^{2}}=\sqrt{7}$；（2）证明：$\because$在$\triangle DCF$和$\triangle ECG$中，$\begin{cases} \angle 1=\angle 2, \\ \angle C=\angle C, \\ CD=CE, \end{cases}$$\therefore \triangle DCF\cong \triangle ECG$（AAS）.$\therefore CF=CG$.$\because CE=CD$，$CE=2CF$，$\therefore CD=2CG$.