2025年暑假综合练习河北人民出版社八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假综合练习河北人民出版社八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
3. 已知 $ a = \sqrt{2} $,求代数式 $ \left( \frac{1}{a - 1} - \frac{1}{a + 1} \right) \cdot \frac{a^2 - 1}{a} $ 的值。
答案:
解:原式=$\frac{2}{a}$. 当$a=\sqrt{2}$时,原式=$\sqrt{2}$.
4. 花农要将规格相同的 $ 800 $ 件水仙花运往 $ A $,$ B $,$ C $ 三地销售,要求运往 $ C $ 地的件数是运往 $ A $ 地件数的 $ 3 $ 倍,各地的运费如下表所示:
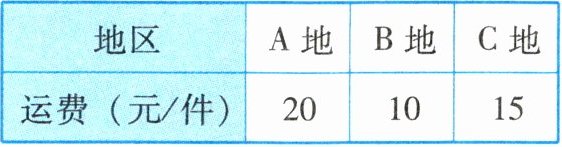
(1)设运往 $ A $ 地的水仙花的件数为 $ x $,总运费为 $ y $(元),试写出 $ y $ 与 $ x $ 的函数关系式;
(2)若总运费不超过 $ 12000 $ 元,则最多可运往 $ A $ 地多少件水仙花?

(1)设运往 $ A $ 地的水仙花的件数为 $ x $,总运费为 $ y $(元),试写出 $ y $ 与 $ x $ 的函数关系式;
(2)若总运费不超过 $ 12000 $ 元,则最多可运往 $ A $ 地多少件水仙花?
答案:
(1)若运往A地的水仙花的件数为x,则运往C地的件数为3x,运往B地的件数为800-4x,由题意得:$y=20x+10(800-4x)+45x$,$y=25x+8000$;(2)
∵ $y\leqslant 12000$,
∴ $25x+8000\leqslant 12000$,解得:$x\leqslant 160$.
∴ 若总运费不超过12000元,最多可运往A地160件水仙花.
∵ $y\leqslant 12000$,
∴ $25x+8000\leqslant 12000$,解得:$x\leqslant 160$.
∴ 若总运费不超过12000元,最多可运往A地160件水仙花.
5. 如图 $ 3 - 9 $ 所示,在菱形 $ ABCD $ 中,$ AB = 2 $,$ \angle DAB = 60^{\circ} $,点 $ E $ 是 $ AD $ 边的中点,点 $ M $ 是 $ AB $ 边上的一个动点(不与点 $ A $ 重合),延长 $ ME $ 交 $ CD $ 的延长线于点 $ N $,连接 $ MD $,$ AN $。
(1)求证:四边形 $ AMDN $ 是平行四边形;
(2)当 $ AM $ 的长度为何值时,四边形 $ AMDN $ 是矩形?请说明理由。
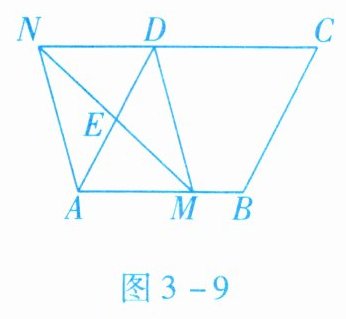
(1)求证:四边形 $ AMDN $ 是平行四边形;
(2)当 $ AM $ 的长度为何值时,四边形 $ AMDN $ 是矩形?请说明理由。

答案:
(1)证明:
∵ 四边形ABCD是菱形,
∴ ND//AM.
∴ ∠NDE=∠MAE,∠DNE=∠AME.
∵ 点E是AD的中点,
∴ DE=AE.在△NDE和△MAE中,$\left\{\begin{array}{l} ∠NDE=∠MAE,\\ ∠DNE=∠AME,\\ DE=AE.\end{array}\right.$
∴ △NDE≌△MAE(AAS)
∴ ND=MA.
∴ 四边形AMDN是平行四边形;(2)解:AM=1.理由如下:
∵ 四边形ABCD是菱形,
∴ AD=AB=2.
∵ 平行四边形AMDN是矩形,
∴ DM⊥AB,即∠DMA=90°.
∵ ∠DAB=60°,
∴ ∠ADM=30°.
∴ $AM=\frac{1}{2}AD=1$.
∵ 四边形ABCD是菱形,
∴ ND//AM.
∴ ∠NDE=∠MAE,∠DNE=∠AME.
∵ 点E是AD的中点,
∴ DE=AE.在△NDE和△MAE中,$\left\{\begin{array}{l} ∠NDE=∠MAE,\\ ∠DNE=∠AME,\\ DE=AE.\end{array}\right.$
∴ △NDE≌△MAE(AAS)
∴ ND=MA.
∴ 四边形AMDN是平行四边形;(2)解:AM=1.理由如下:
∵ 四边形ABCD是菱形,
∴ AD=AB=2.
∵ 平行四边形AMDN是矩形,
∴ DM⊥AB,即∠DMA=90°.
∵ ∠DAB=60°,
∴ ∠ADM=30°.
∴ $AM=\frac{1}{2}AD=1$.
查看更多完整答案,请扫码查看


