15. 如图,已知四边形 $ ABCD $ 是平行四边形, $ P $ 为 $ DC $ 延长线上一点, $ AP $ 分别交 $ BD $, $ BC $于点 $ M $, $ N $。
(1) 求证: $ AM^2 = MN \cdot MP $;
(2) 若 $ AD = 6 $, $ DC : CP = 2 : 1 $,求 $ BN $的长。
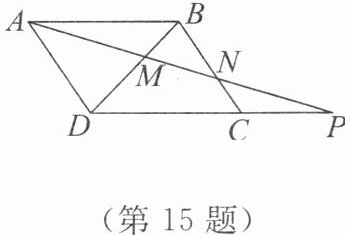
(1) 求证: $ AM^2 = MN \cdot MP $;
(2) 若 $ AD = 6 $, $ DC : CP = 2 : 1 $,求 $ BN $的长。

答案:
提示:
(1)通过证明$\triangle ADM \backsim \triangle NBM$,$\triangle PDM \backsim \triangle ABM$,可得$\frac{AM}{MN}=\frac{DM}{BM}=\frac{PM}{AM}$,即可得结论.
(2)通过证明$\triangle PCN \backsim \triangle PDA$,可得$\frac{PC}{PD}=\frac{NC}{AD}$,可求$NC=2$,即可求得$BN$的长为 4.
(1)通过证明$\triangle ADM \backsim \triangle NBM$,$\triangle PDM \backsim \triangle ABM$,可得$\frac{AM}{MN}=\frac{DM}{BM}=\frac{PM}{AM}$,即可得结论.
(2)通过证明$\triangle PCN \backsim \triangle PDA$,可得$\frac{PC}{PD}=\frac{NC}{AD}$,可求$NC=2$,即可求得$BN$的长为 4.
16. 定义:在 $ \triangle ABC $ 中,点 $ D $, $ E $, $ F $ 分别是边 $ AB $, $ BC $, $ CA $ 上的动点,若 $ \triangle DEF \sim \triangle ABC $(点 $ D $, $ E $, $ F $ 的对应点分别为点 $ A $, $ B $, $ C $),则称 $ \triangle DEF $ 是 $ \triangle ABC $ 的“子三角形”。
(1) 如图①, $ \triangle ABC $ 是等边三角形,点 $ D $, $ E $, $ F $ 分别是边 $ AB $, $ BC $, $ CA $ 上的动点,且 $ AD = BE = CF $。求证: $ \triangle DEF $ 是 $ \triangle ABC $ 的“子三角形”;
(2) 如图②, $ \triangle DEF $ 是 $ \triangle ABC $ 的子三角形,且 $ AB = AC $, $ \angle A = 90° $,若 $ BE = \sqrt{2} $,求 $ CF $和 $ AD $ 的长。
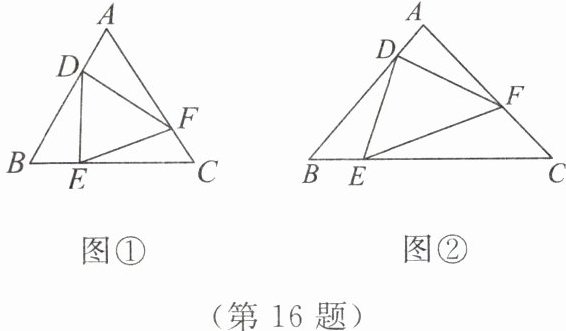
(1) 如图①, $ \triangle ABC $ 是等边三角形,点 $ D $, $ E $, $ F $ 分别是边 $ AB $, $ BC $, $ CA $ 上的动点,且 $ AD = BE = CF $。求证: $ \triangle DEF $ 是 $ \triangle ABC $ 的“子三角形”;
(2) 如图②, $ \triangle DEF $ 是 $ \triangle ABC $ 的子三角形,且 $ AB = AC $, $ \angle A = 90° $,若 $ BE = \sqrt{2} $,求 $ CF $和 $ AD $ 的长。

答案:
解:
(1)如图①,通过证明$\triangle DAF \cong \triangle EBD \cong \triangle FCE$,可得到$DE=EF=DF$,即$\triangle DEF$是等边三角形,从而可得$\triangle DEF \backsim \triangle ABC$. 因此$\triangle DEF$是$\triangle ABC$的“子三角形”.

(2)如图②,作$EH \perp AB$于点$H$.
由$\triangle DEF$是$\triangle ABC$的子三角形,知$\triangle DEF \backsim \triangle ABC$,得$DE=DF$,$\angle EDF=90°$,所以有$\angle ADF+\angle AFD=90°$,$\angle ADF+\angle EDH=90°$,继而得到$\angle EDH=\angle AFD$,因此$\triangle DEH \cong \triangle FDA$,所以$AD=HE$.
所以$AD=HE=\frac{\sqrt{2}}{2} × \sqrt{2}=1$.
由$\triangle BDE \backsim \triangle CEF$,得$\frac{BE}{CF}=\frac{DE}{EF}=\frac{\sqrt{2}}{2}$,求得$CF=2$.

解:
(1)如图①,通过证明$\triangle DAF \cong \triangle EBD \cong \triangle FCE$,可得到$DE=EF=DF$,即$\triangle DEF$是等边三角形,从而可得$\triangle DEF \backsim \triangle ABC$. 因此$\triangle DEF$是$\triangle ABC$的“子三角形”.

(2)如图②,作$EH \perp AB$于点$H$.
由$\triangle DEF$是$\triangle ABC$的子三角形,知$\triangle DEF \backsim \triangle ABC$,得$DE=DF$,$\angle EDF=90°$,所以有$\angle ADF+\angle AFD=90°$,$\angle ADF+\angle EDH=90°$,继而得到$\angle EDH=\angle AFD$,因此$\triangle DEH \cong \triangle FDA$,所以$AD=HE$.
所以$AD=HE=\frac{\sqrt{2}}{2} × \sqrt{2}=1$.
由$\triangle BDE \backsim \triangle CEF$,得$\frac{BE}{CF}=\frac{DE}{EF}=\frac{\sqrt{2}}{2}$,求得$CF=2$.

查看更多完整答案,请扫码查看


