1. 下列各组长度的四条线段(单位:cm)成比例的是(
A.3,6,5,4
B.3,4,6,9
C.1,5,2,3
D.2,4,5,10
D
).A.3,6,5,4
B.3,4,6,9
C.1,5,2,3
D.2,4,5,10
答案:
D
2. 已知a,b,c,d是成比例线段,其中a= 2 cm,b= 3 cm,c= 6 cm,则d的长度为(
A.4 cm
B.5 cm
C.6 cm
D.9 cm
D
).A.4 cm
B.5 cm
C.6 cm
D.9 cm
答案:
D
3. 在比例尺是1:200 000的地图上,A,B两地间的距离为4 cm,则A,B两地的实际距离是(
A.8 km
B.5 km
C.80 km
D.0. 5 km
A
).A.8 km
B.5 km
C.80 km
D.0. 5 km
答案:
A
4. 如果2a= 3b(b≠0),那么a:b=
3∶2
.
答案:
3∶2
5. 已知线段a= 3,b= 4,c= 6,且线段a,c,b,d成比例,则d=
8
.
答案:
8
6. 如图,在等腰直角三角形ABC中,∠C= 90°,则$\frac{AC}{AB}$=
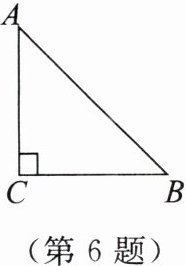
$1:\sqrt{2}$
.
答案:
$1:\sqrt{2}$
7. 如图,点C,D是线段AB上两点,AC= 1 cm,CD= 2 cm,DB= 3 cm. 请找出图中能成比例的四条线段,并用比例式表示.(只要写出符合条件的一组线段即可)


答案:
$\frac{AC}{CD}=\frac{AD}{AB}$(答案不唯一)
8. 若点P在线段AB上,点Q在线段AB的延长线上,AB= 10,$\frac{AP}{BP}= \frac{AQ}{BQ}= \frac{3}{2}$. 求线段PQ的长.
答案:
24.
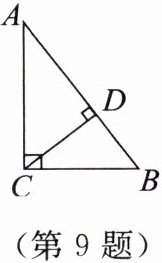
9. 如图,在Rt△ABC中,∠ACB= 90°,CD⊥AB于点D.
(1)当AC= 4,AB= 5时,求线段BC与CD的长,并判断线段CD,BC,AC与AB是不是成比例线段;
(2)线段CD,BC,AC与AB一定是成比例线段吗? 为什么?
(1)当AC= 4,AB= 5时,求线段BC与CD的长,并判断线段CD,BC,AC与AB是不是成比例线段;
(2)线段CD,BC,AC与AB一定是成比例线段吗? 为什么?

答案:
解:
(1)$BC=3$,$CD=2.4$,是成比例线段,且$\frac{CD}{BC}=\frac{AC}{AB}$.
(2)一定是.理由略.
(1)$BC=3$,$CD=2.4$,是成比例线段,且$\frac{CD}{BC}=\frac{AC}{AB}$.
(2)一定是.理由略.
查看更多完整答案,请扫码查看


