1. 如图,分别旋转两个标准的转盘,两个转盘分别被分成两等份和三等份,则转盘所转到的两个数字之积为奇数的概率是(
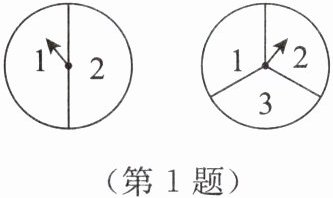
A.$\frac{3}{5}$
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{1}{6}$
B
)。
A.$\frac{3}{5}$
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{1}{6}$
答案:
B
2. 一个不透明的盒中装有红、黄、绿小球各 1 个(小球形状、大小、质地一样),从盒中随机摸取 1 个小球然后放回,再随机摸取 1 个小球,则两次摸取的小球中只有一次是红球的概率为(
A.$\frac{1}{5}$
B.$\frac{4}{9}$
C.$\frac{5}{9}$
D.$\frac{2}{3}$
B
)。A.$\frac{1}{5}$
B.$\frac{4}{9}$
C.$\frac{5}{9}$
D.$\frac{2}{3}$
答案:
B
3. 为积极响应“无偿献血,传递温暖”的号召,某高校一寝室的 4 个同学也参与到爱心献血的活动中。他们中有 2 个 A 型血,1 个 B 型血,1 个 O 型血,现从该寝室随机抽取 2 个同学参与第一批次献血,则这 2 个同学都是 A 型血的概率为
$\frac{1}{6}$
。
答案:
$\frac{1}{6}$
4. 不透明的布袋里有 2 个黄球、3 个红球、5 个白球,它们除颜色外其他都相同,则从布袋中任意摸出 1 个球,其恰好为红球的概率是
$\frac{3}{10}$
。
答案:
$\frac{3}{10}$
5. 如图,有 4 张背面相同的纸牌 A,B,C,D,其正面分别画有 4 个不同的几何图形。将这 4 张纸牌背面朝上洗匀后先由小明从中任意摸出 1 张,放回洗匀后再由小敏从中任意摸出 1 张,则“小明所摸纸牌上的图形是中心对称图形,小敏所摸纸牌上的图形是轴对称图形”的概率为
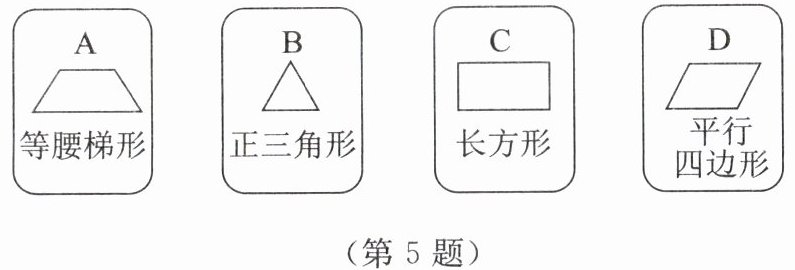
$\frac{3}{8}$
。(既是中心对称图形又是轴对称图形的可以认为是这两种中的任意一种图形)
答案:
$\frac{3}{8}$
6. 周末李老师去逛街,发现某商场消费满 1000 元就能获得一次抽奖机会,李老师消费 1200 元后来到抽奖台,台上放着一个不透明的抽奖箱,里面放有规格完全相同的四个小球,球上分别标有 1,2,3,4 四个数字。主持人让李老师连续不放回抽两次,每次抽取一个小球,如果两个小球上的数字均为奇数则可中奖,那么李老师中奖的概率是
$\frac{1}{6}$
。
答案:
$\frac{1}{6}$
7. 学生甲与学生乙学习概率初步知识后设计了如下游戏:学生甲手中有 6,8,9 三张扑克牌,学生乙手中有 5,7,10 三张扑克牌,每人从自己手中取一张牌进行比较,数字大的本局获胜,每次取出的牌不能放回。
(1) 若每人随机取出手中的一张牌进行比较,请列举出所有的情况;
(2) 求学生乙本局获胜的概率。
(1) 若每人随机取出手中的一张牌进行比较,请列举出所有的情况;
(2) 求学生乙本局获胜的概率。
答案:
7. 解:
(1)画树状图如下.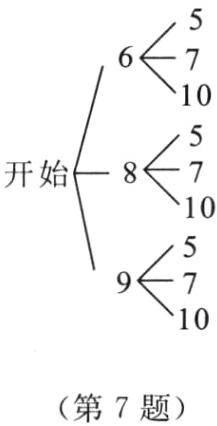
共有 9 种等可能的情况.
(2)学生乙本局获胜的情况有 4 种,所以学生乙本局获胜的概率为 $\frac{4}{9}$.
7. 解:
(1)画树状图如下.

共有 9 种等可能的情况.
(2)学生乙本局获胜的情况有 4 种,所以学生乙本局获胜的概率为 $\frac{4}{9}$.
查看更多完整答案,请扫码查看


