1. 下列条件中可以判定$\triangle ABC \backsim \triangle A^{\prime} B^{\prime} C^{\prime}$的是(
A.$\frac{AB}{AC}= \frac{A^{\prime} B^{\prime}}{A^{\prime} C^{\prime}}$
B.$\frac{AB}{AC}= \frac{A^{\prime} B^{\prime}}{A^{\prime} C^{\prime}}, \angle B= \angle B^{\prime}$
C.$\frac{AB}{AC}= \frac{A^{\prime} B^{\prime}}{A^{\prime} C^{\prime}}, \angle A= \angle A^{\prime}$
D.$\frac{AB}{A^{\prime} B^{\prime}}=\frac{AC}{A^{\prime} C^{\prime}}$
C
)。A.$\frac{AB}{AC}= \frac{A^{\prime} B^{\prime}}{A^{\prime} C^{\prime}}$
B.$\frac{AB}{AC}= \frac{A^{\prime} B^{\prime}}{A^{\prime} C^{\prime}}, \angle B= \angle B^{\prime}$
C.$\frac{AB}{AC}= \frac{A^{\prime} B^{\prime}}{A^{\prime} C^{\prime}}, \angle A= \angle A^{\prime}$
D.$\frac{AB}{A^{\prime} B^{\prime}}=\frac{AC}{A^{\prime} C^{\prime}}$
答案:
C
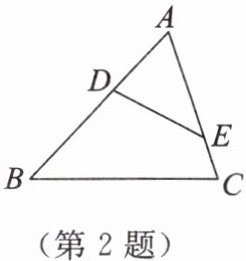
2. 如图,在$\triangle ABC$中,点$D, E分别在边AB$,$AC$上,下列条件中能判断$\triangle ABC \backsim \triangle AED$的是(
①$\angle AED= \angle B$;②$\angle ADE= \angle C$;③$\frac{AD}{AE}= \frac{AC}{AB}$;④$\frac{AD}{AB}= \frac{AE}{AC}$。
A.①②
B.①②③
C.①②④
D.①②③④
B
)。①$\angle AED= \angle B$;②$\angle ADE= \angle C$;③$\frac{AD}{AE}= \frac{AC}{AB}$;④$\frac{AD}{AB}= \frac{AE}{AC}$。

A.①②
B.①②③
C.①②④
D.①②③④
答案:
B
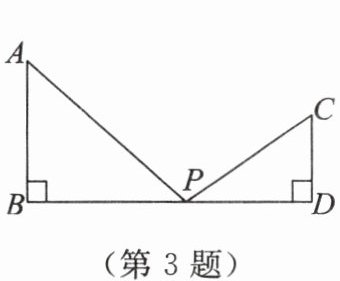
3. 如图,$AB \perp BD, CD \perp BD, AB= 6, CD= 4$,$BD= 14$。点$P在BD$上移动,当以$P, C, D为顶点的三角形与\triangle ABP$相似时,则$PB$的长为
8.4 或 2 或 12
。
答案:
8.4 或 2 或 12
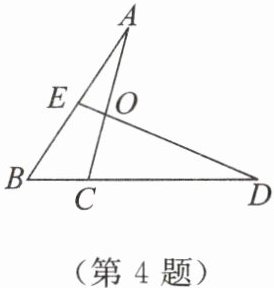
4. 如图,已知$AB= 6, BE= 3, BD= 9$,当$BC= $
2
时,$\triangle ABC \backsim \triangle DBE$,此时,$\angle A= $∠D
,$\triangle AOE \backsim$△DOC
。
答案:
2,∠D,△DOC
5. 在$\triangle ABC$中,$AB= 6, AC= 5$,点$D在边AB$上,且$AD= 2$,点$E在边AC$上,当$AE= $
$\frac{5}{3}$或$\frac{12}{5}$
时,以$A, D, E为顶点的三角形与\triangle ABC$相似。
答案:
$\frac{5}{3}$或$\frac{12}{5}$
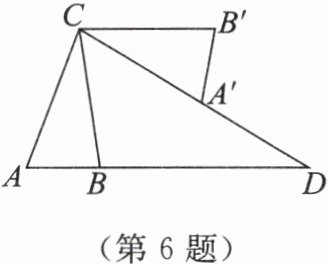
6. 如图,在$\triangle ABC$中,$AB= 2, AC= 4$,将$\triangle ABC绕点C按逆时针方向旋转得到\triangle A^{\prime} B^{\prime} C$,分别延长$AB, CA^{\prime}$,相交于点$D$,线段$BD的长为6$。
(1) 求证:$\triangle ABC \backsim \triangle ACD$;
(2)$CB^{\prime}与AB$平行吗?为什么?
(1) 求证:$\triangle ABC \backsim \triangle ACD$;
(2)$CB^{\prime}与AB$平行吗?为什么?

答案:
(1)略.
(2)平行. 理由略.
(1)略.
(2)平行. 理由略.
7. 如图,在$Rt \triangle ABC$中,$\angle ABC= 90^{\circ}, AB= 8$,$BC= 6$,点$M, P分别从点B和点C$同时出发,点$M沿BC向点C$运动,点$P沿CA向点A$运动,当任一点到达终点即停止运动,$M, P两点的运动速度均为1$个单位长度/s,运动时间为$t$s。求当$t$为何值时,$\triangle MCP与\triangle ABC$相似。
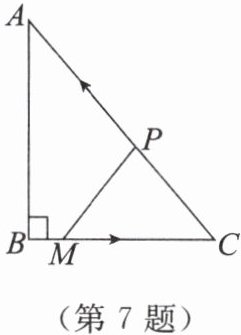

答案:
$t=\frac{9}{4}s$或$\frac{15}{4}s$.
查看更多完整答案,请扫码查看


