1. 如图,在菱形 $ABCD$ 中,$AE\perp BC$ 于点 $E$。若 $S_{菱形ABCD}= 48$,且 $AE = 6$,则菱形的边长为(

A.$12$
B.$8$
C.$4$
D.$2$
B
)。
A.$12$
B.$8$
C.$4$
D.$2$
答案:
B
2. 如图,$O$ 是矩形 $ABCD$ 的对角线 $AC$ 的中点,$M$ 是 $AD$ 的中点。若 $AB = 5$,$AD = 12$,则四边形 $ABOM$ 的周长为(

A.$18$
B.$20$
C.$22$
D.$24$
B
)。
A.$18$
B.$20$
C.$22$
D.$24$
答案:
B
3. 如图,$BD$ 是菱形 $ABCD$ 的一条对角线。若 $\angle ABD = 65^{\circ}$,则 $\angle A= $

50°
。
答案:
50°
4. 如图,在 $\triangle ABC$ 中,已知 $\angle ACB = 90^{\circ}$,$\angle A = 30^{\circ}$,$BC = 6$,$D$ 为斜边 $AB$ 上一点,以 $CD$,$CB$ 为边作平行四边形 $CDEB$,当 $AD = $

6
时,平行四边形 $CDEB$ 为菱形。
答案:
6
5. 如图,在 $□ ABCD$ 中,$E$ 为 $BC$ 边上一点,以 $AE$ 为边作矩形 $AEFG$。若 $\angle BAE = 40^{\circ}$,$\angle CEF = 15^{\circ}$,则 $\angle D$ 的大小为
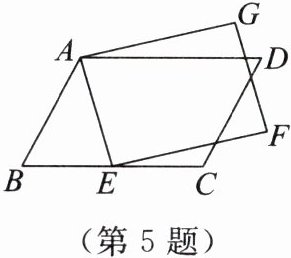
65°
。
答案:
65°
6. 如图,正方形 $ABCD$ 的面积为 $5$,正方形 $BEFG$ 的面积为 $3$,那么 $\triangle GCE$ 的面积是

$\frac{\sqrt{15}}{2}-\frac{3}{2}$
。
答案:
$\frac{\sqrt{15}}{2}-\frac{3}{2}$
7. 如图,在正方形 $ABCD$ 中,点 $E$ 在 $BC$ 边的延长线上,点 $F$ 在 $CD$ 边的延长线上,且 $CE = DF$,连接 $AE$ 和 $BF$,相交于点 $M$。求证:$AE = BF$。


答案:
提示:证明△AEB≌△BFC(SAS)即可.
8. 如图,在矩形 $ABCD$ 中,对角线 $AC$,$BD$ 交于点 $O$,$\angle BAC = 60^{\circ}$,过点 $O$ 作 $OM\perp AD$ 于点 $M$,求证:$OM= \frac{1}{2}OB$。


答案:
提示:根据矩形的性质及∠BAC的度数确定△ABO是等边三角形,然后根据三角形的中位线定理证得结论.
查看更多完整答案,请扫码查看


