1. 下列三个三角形中相似的是(
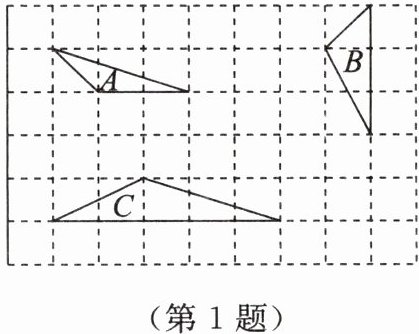
A.$ A $ 与 $ B $
B.$ A $ 与 $ C $
C.$ B $ 与 $ C $
D.$ A,B,C $ 都相似
B
)。
A.$ A $ 与 $ B $
B.$ A $ 与 $ C $
C.$ B $ 与 $ C $
D.$ A,B,C $ 都相似
答案:
B
2. 下列条件中,不能判断 $ \triangle ABC $ 与 $ \triangle DEF $ 相似的是(
A.$ \angle A= \angle D,\angle B= \angle F $
B.$ \frac{BC}{EF}= \frac{AC}{DF} $ 且 $ \angle B= \angle D $
C.$ \frac{AB}{DE}= \frac{BC}{EF}= \frac{AC}{DF} $
D.$ \frac{AB}{DE}= \frac{AC}{DF} $ 且 $ \angle A= \angle D $
B
)。A.$ \angle A= \angle D,\angle B= \angle F $
B.$ \frac{BC}{EF}= \frac{AC}{DF} $ 且 $ \angle B= \angle D $
C.$ \frac{AB}{DE}= \frac{BC}{EF}= \frac{AC}{DF} $
D.$ \frac{AB}{DE}= \frac{AC}{DF} $ 且 $ \angle A= \angle D $
答案:
B
3. 在 $ \triangle ABC $ 与 $ \triangle A'B'C' $ 中,已知 $ AB = 6,BC = 12,AC = 15,A'B' = 8,B'C' = 16 $,则当 $ A'C' = $
20
时,$ \triangle ABC\sim\triangle A'B'C' $。
答案:
20
4. 如图,在平面直角坐标系中有两点 $ A(4,0) $,$ B(0,2) $,如果点 $ C $ 在 $ x $ 轴上($ C $ 与 $ A $ 不重合),那么当点 $ C $ 的坐标为
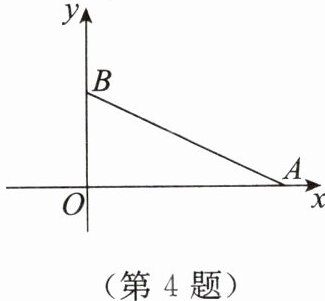
(-1,0)或(1,0)
时,$ \triangle BOC\sim\triangle AOB $。
答案:
(-1,0)或(1,0)
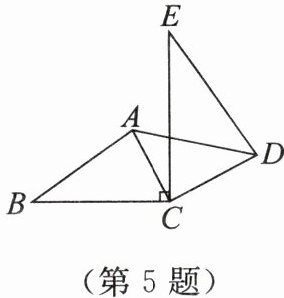
5. 如图,在 $ \triangle ABC $ 和 $ \triangle DEC $ 中,$ AB = 6,AC = 4,BC = 8,CE = 12,CD = 6,DE = 9,CE\perp BC $。
(1) 求证:$ \triangle ABC\sim\triangle DEC $;
(2) 求 $ AD $ 的长。
(1) 求证:$ \triangle ABC\sim\triangle DEC $;
(2) 求 $ AD $ 的长。

答案:
(1)略.
(2)$2\sqrt{13}$.
(1)略.
(2)$2\sqrt{13}$.
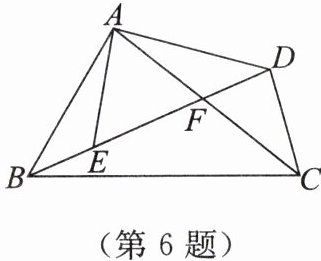
6. 如图,在四边形 $ ABCD $ 中,$ AC,BD $ 相交于点 $ F $,点 $ E $ 在 $ BD $ 上,且 $ \frac{AB}{AE}= \frac{BC}{ED}= \frac{AC}{AD} $。
(1) $ \angle BAE $ 与 $ \angle CAD $ 相等吗?为什么?
(2) 试判断 $ \triangle ABE $ 与 $ \triangle ACD $ 是否相似,并说明理由。
(1) $ \angle BAE $ 与 $ \angle CAD $ 相等吗?为什么?
(2) 试判断 $ \triangle ABE $ 与 $ \triangle ACD $ 是否相似,并说明理由。

答案:
(1)相等,理由略.
(2)相似,理由略.
(1)相等,理由略.
(2)相似,理由略.
查看更多完整答案,请扫码查看


