1. 如图,某一时刻,一根长为 $ 1.6 \, m $ 的标杆 $ DF $ 在阳光下的影长 $ EF $ 的长度为 $ 0.4 \, m $,同一时刻同一地点测得某旗杆的影长 $ BC $ 的长度为 $ 5 \, m $,则该旗杆 $ AC $ 的高度为(

A.$ 1.25 \, m $
B.$ 10 \, m $
C.$ 20 \, m $
D.$ 8 \, m $
C
).
A.$ 1.25 \, m $
B.$ 10 \, m $
C.$ 20 \, m $
D.$ 8 \, m $
答案:
C
2. 如图,某校数学兴趣小组利用标杆 $ BE $ 测量图书馆的高度. 已知标杆 $ BE $ 高 $ 1.5 \, m $,测得 $ AB = 1.2 \, m $,$ BC = 12.8 \, m $,则图书馆 $ CD $ 的高度是(

A.$ 17.5 \, m $
B.$ 17 \, m $
C.$ 16.5 \, m $
D.$ 18 \, m $
A
).
A.$ 17.5 \, m $
B.$ 17 \, m $
C.$ 16.5 \, m $
D.$ 18 \, m $
答案:
A
3. 如图是一位同学设计的用手电筒来测量某古城墙高度的示意图. 点 $ P $ 处放一水平的平面镜,光线从点 $ A $ 出发经平面镜反射后刚好到古城墙 $ CD $ 的顶端 $ C $ 处. 已知 $ AB \perp BD $,$ CD \perp BD $,测得 $ AB = 2 \, m $,$ BP = 3 \, m $,$ PD = 15 \, m $,那么该古城墙 $ CD $ 的高度是
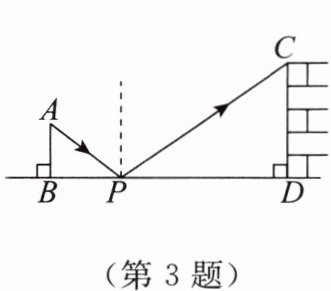
10
$ m $.
答案:
10
4. 《九章算术》中记载了一种测量井深的方法. 如图所示,在井口 $ B $ 处立一根垂直于井口的木杆 $ BD $,从木杆的顶端 $ D $ 观察井水水岸 $ C $,视线 $ DC $ 与井口的直径 $ AB $ 交于点 $ E $,如果测得 $ AB = 1.6 \, m $,$ BD = 1 \, m $,$ BE = 0.2 \, m $,那么 $ AC $ 为

7
$ m $.
答案:
7
5. 如图,为了测量一个大峡谷的宽度,地质勘探人员在对面的岩石上观察到一个特别明显的标志点 $ O $,再在他们所在的这一侧选点 $ A $,$ B $,$ D $,使 $ AB \perp AO $,$ DB \perp AB $,然后确定 $ DO $ 和 $ AB $ 的交点 $ C $,测得 $ AC = 120 \, m $,$ CB = 60 \, m $,$ BD = 50 \, m $,请你帮助他们算出大峡谷的宽 $ AO $.
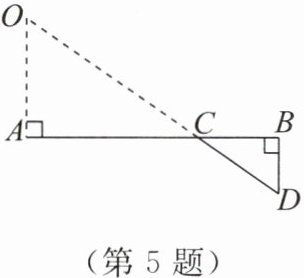

答案:
100m.
6. 如图,小华和同伴发现在某地小山坡的点 $ E $ 处有一棵小桃树,他们想利用皮尺、测倾器和平面镜测量小桃树到山脚下的距离(即 $ DE $ 的长度). 小华站在点 $ B $ 处,让同伴移动平面镜至点 $ C $ 处,此时小华在平面镜内可以看到点 $ E $,且测得 $ BC = 6 \, m $,$ CD = 24 \, m $,$ \angle CDE = 135° $,已知小华的身高 $ AB = 1.5 \, m $. 请根据以上数据求 $ DE $ 的长度(结果保留根号).


答案:
提示:如图,过点E作EF⊥BC于点F,由∠CDE=135°可得∠EDF=45°.设EF=xm,则DF=xm,DE=$\sqrt{2}$xm.根据∠B=∠EFC=90°,∠ACB=∠ECD,可证得△ABC∽△EFC,所以$\frac{AB}{EF}=\frac{BC}{FC}$,即$\frac{1.5}{x}=\frac{6}{24+x}$,解得x=8,继而求得DE=$8\sqrt{2}$.

提示:如图,过点E作EF⊥BC于点F,由∠CDE=135°可得∠EDF=45°.设EF=xm,则DF=xm,DE=$\sqrt{2}$xm.根据∠B=∠EFC=90°,∠ACB=∠ECD,可证得△ABC∽△EFC,所以$\frac{AB}{EF}=\frac{BC}{FC}$,即$\frac{1.5}{x}=\frac{6}{24+x}$,解得x=8,继而求得DE=$8\sqrt{2}$.

查看更多完整答案,请扫码查看


