《2025年课堂精练九年级数学上册北师大版福建专版》

1. 方程 $x^{2}= 4x$ 的解是$x_{1}=0,x_{2}=4$.

答案： $x_{1}=0,x_{2}=4$

2. 方程 $x(x - 2)= x$ 的解是$x_{1}=0,x_{2}=3$.

答案： $x_{1}=0,x_{2}=3$

3. 方程 $x(x - 1)= 2$ 的解是$x_{1}=2,x_{2}=-1$.

答案： $x_{1}=2,x_{2}=-1$

4. 请写出一个两根分别是 1 和 -2 的一元二次方程：$x^{2}+x-2=0$（答案不唯一）.

答案： $x^{2}+x-2=0$（答案不唯一）

5. 用因式分解法解下列方程：
(1) $(x + 1)(2x - 3)= 0$；
(2) $4x(3x + 1)= 3x + 1$；
(3) $(2 - 3x)-(3x - 2)^{2}= 0$；
(4) $(x + 1)^{2}= (1 - 2x)^{2}$.

答案：
(1)$x_{1}=\frac{3}{2},x_{2}=-1$.
(2)$x_{1}=\frac{1}{4},x_{2}=-\frac{1}{3}$.
(3)$x_{1}=\frac{2}{3},x_{2}=\frac{1}{3}$.
(4)$x_{1}=0,x_{2}=2$.

6. 小明在解一元二次方程 $3x^{2}-8x(x - 2)= 0$ 时是这样做的：
$\begin{array}{r}3x^{2}-8x(x - 2)= 0 \\解:3x - 8x - 2= 0 ……\quad 第一步 \\-5x - 2= 0 ……\quad 第二步 \\-5x= 2 ……\quad 第三步 \\x= -\frac{2}{5} ……\quad 第四步\end{array} $
(1) 小明的解法从第一步开始出现错误,此题的正确结果是$x_{1}=0,x_{2}=\frac{16}{5}$；
(2) 用因式分解法解方程 $x(2x - 1)= 3(2x - 1)$.
$x_{1}=\frac{1}{2},x_{2}=3$

答案：
(1)一,$x_{1}=0,x_{2}=\frac{16}{5}$.
(2)$x_{1}=\frac{1}{2},x_{2}=3$.

7. 若多项式 $x^{2}+px + q$ 因式分解的结果是 $(x + m)(x + n)$,则关于 $x$ 的方程 $x^{2}+px + q= 0$ 的根为$x_{1}=-m,x_{2}=-n$.

答案： $x_{1}=-m,x_{2}=-n$

8. 对于实数 $a,b$ 定义运算“$*$”如下：$a*b= (a + b)^{2}-(a - b)^{2}$. 若 $(x + 2)*(x - 3)= -24$,求 $x$ 的值.

答案： x的值为0或1.

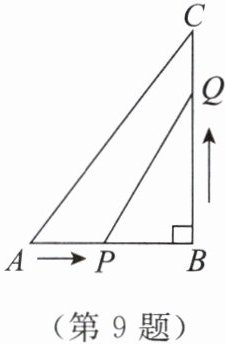
9. 如图,在 $\triangle ABC$ 中,$\angle B= 90^{\circ}$,$AB = 5\ cm$,$BC = 7\ cm$. 点 $P$ 从点 $A$ 开始沿 $AB$ 边向点 $B$ 以 $1\ cm/s$ 的速度移动,点 $Q$ 从点 $B$ 开始沿 $BC$ 边向点 $C$ 以 $2\ cm/s$ 的速度移动. 如果 $P,Q$ 分别从 $A,B$ 同时出发,那么几秒后,四边形 $APQC$ 的面积等于 $11.5\ cm^{2}$?

答案： 2 s或3 s.