1. 下列方程中,是关于 $ x $ 的一元二次方程的是(
A.$ ax^{2}+bx+c = 0 $
B.$ \frac{1}{x^{2}}+\frac{1}{x}-2 = 0 $
C.$ 3(x + 1)^{2}= 2(x + 1) $
D.$ x^{2}+2x = x^{2}-1 $
C
).A.$ ax^{2}+bx+c = 0 $
B.$ \frac{1}{x^{2}}+\frac{1}{x}-2 = 0 $
C.$ 3(x + 1)^{2}= 2(x + 1) $
D.$ x^{2}+2x = x^{2}-1 $
答案:
C
2. 若方程 $ (m + 2)x^{|m|}+3x - 1 = 0 $ 是关于 $ x $ 的一元二次方程,则(
A.$ m = 2 $
B.$ m = -2 $
C.$ m = \pm 2 $
D.$ m \neq \pm 2 $
A
).A.$ m = 2 $
B.$ m = -2 $
C.$ m = \pm 2 $
D.$ m \neq \pm 2 $
答案:
A
3. 方程 $ 2x(x - 1)= 3(x + 5)-4 $ 的一般形式是
2x²-5x-11=0
,其中二次项系数是2
,一次项系数是-5
,常数项是-11
.
答案:
2x²-5x-11=0,2,-5,-11
4. 已知两个数的差为 3,它们的平方和是 65,设较小的数为 $ x $,则可列方程:
x²+(x+3)²=65
.
答案:
x²+(x+3)²=65
5. 有一个面积是 $ 15\mathrm{cm}^{2} $ 的矩形,当长增加 $ 1\mathrm{cm} $,宽增加 $ 3\mathrm{cm} $ 时,恰好变成一个正方形. 若设这个正方形的边长为 $ x\mathrm{cm} $,根据题意,则可列方程:
(x-1)(x-3)=15
,把它化成一般形式为x²-4x-12=0
.
答案:
(x-1)(x-3)=15,x²-4x-12=0
6. 已知 $ (a - 2)x^{b}-3bx + 2 = 0 $ 是关于 $ x $ 的一元二次方程,则(
A.$ a \neq 0,b = 2 $
B.$ a \neq 2,b = 2 $
C.$ a \neq 0,b \neq 0 $
D.$ a \neq 2,b \neq 0 $
B
).A.$ a \neq 0,b = 2 $
B.$ a \neq 2,b = 2 $
C.$ a \neq 0,b \neq 0 $
D.$ a \neq 2,b \neq 0 $
答案:
B
7. 求当 $ m $ 是何值时,关于 $ x $ 的方程 $ (m^{2}+2)x^{2}+(m - 1)x - 4 = 3x^{2} $,
(1)是一元二次方程;
(2)是一元一次方程.
(1)是一元二次方程;
(2)是一元一次方程.
答案:
(1)m≠±1.
(2)m=-1.
(1)m≠±1.
(2)m=-1.
8. 根据题意,列出一元二次方程.
(1)已知三个连续奇数的平方和为 155,求这三个数.
(2)在一块长方形薄钢片的四个角上截去四个相同的小正方形,然后把四边折起来,就可以做成一个没有盖的长方体盒子. 如图①所示,用一块长 $ 80\mathrm{cm} $、宽 $ 60\mathrm{cm} $ 的薄钢片,在四个角上截去四个相同的小正方形,然后做成如图②所示的底面积为 $ 1500\mathrm{cm}^{2} $ 的没有盖的长方体盒子,求截去的小正方形的边长.
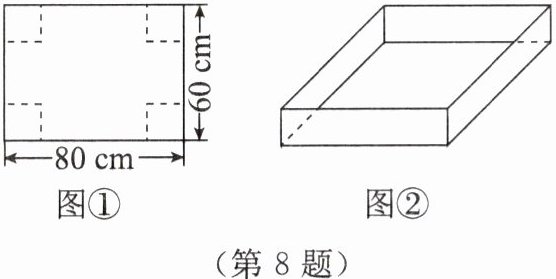
(1)已知三个连续奇数的平方和为 155,求这三个数.
(2)在一块长方形薄钢片的四个角上截去四个相同的小正方形,然后把四边折起来,就可以做成一个没有盖的长方体盒子. 如图①所示,用一块长 $ 80\mathrm{cm} $、宽 $ 60\mathrm{cm} $ 的薄钢片,在四个角上截去四个相同的小正方形,然后做成如图②所示的底面积为 $ 1500\mathrm{cm}^{2} $ 的没有盖的长方体盒子,求截去的小正方形的边长.

答案:
解:
(1)设中间的奇数为x,则(x-2)²+x²+(x+2)²=155.
(2)设截去的小正方形的边长为x cm,则(80-2x)(60-2x)=1500.
(1)设中间的奇数为x,则(x-2)²+x²+(x+2)²=155.
(2)设截去的小正方形的边长为x cm,则(80-2x)(60-2x)=1500.
9. 为了缓解上下学期间学校周边交通拥堵的现状,某社区所有党员自发成立“交通协管志愿小组”,并建立小组微信群. 群里每人都分别给其他人发了一条鼓励的信息,一共产生了 90 条信息,则该社区有多少名党员?若设该社区有 $ x $ 名党员,请列出满足题意的方程.
答案:
x(x-1)=90.
查看更多完整答案,请扫码查看


