1. 如图,在平面直角坐标系中,已知点 $ A $,$ D $ 的坐标分别是 $ (1,0) $,$ (3,0) $,$ \triangle ABC $ 与 $ \triangle DEF $ 位似,原点 $ O $ 是位似中心. 若 $ AB = 1.5 $,则 $ DE $ 的长为(
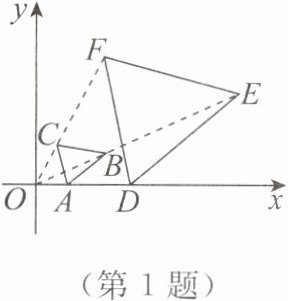
A.$ 2 $
B.$ 3 $
C.$ 4.5 $
D.$ 6 $
C
).
A.$ 2 $
B.$ 3 $
C.$ 4.5 $
D.$ 6 $
答案:
C
2. 如图,线段 $ CD $ 两个端点的坐标分别为 $ C(4,4) $,$ D(6,2) $,以原点 $ O $ 为位似中心,在第一象限内将线段 $ CD $ 缩小为原来的一半后得到线段 $ AB $,则端点 $ A $ 的坐标为(
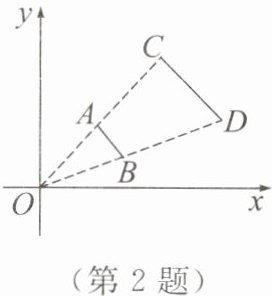
A.$ (2,2) $
B.$ (3,3) $
C.$ (3,1) $
D.$ (4,1) $
A
).
A.$ (2,2) $
B.$ (3,3) $
C.$ (3,1) $
D.$ (4,1) $
答案:
A
3. 如图,在平面直角坐标系中,$ \triangle ABO $ 三个顶点的坐标分别为 $ A(2,4) $,$ B(6,0) $,$ O(0,0) $,以原点 $ O $ 为位似中心,把这个三角形缩小,得到 $ \triangle A'B'O $. 已知点 $ B' $ 的坐标是 $ (3,0) $,则点 $ A' $ 的坐标是
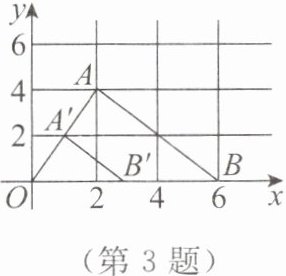
(1,2)
.
答案:
(1,2)
4. 在平面直角坐标系中,$ \triangle ABC $ 和 $ \triangle A_1B_1C_1 $ 的相似比为 $ \frac{1}{2} $,并且是关于原点 $ O $ 的位似图形. 若点 $ A $ 的坐标为 $ (2,4) $,则其对应点 $ A_1 $ 的坐标是
(4,8)或(-4,-8)
.
答案:
(4,8)或(-4,-8)
5. 如图,已知 $ \triangle ABC $ 在平面直角坐标系内,三个顶点的坐标分别为 $ A(0,3) $,$ B(3,4) $,$ C(2,2) $(正方形网格中每个小正方形的边长都是 $ 1 $ 个单位长度).
(1)以点 $ B $ 为位似中心,在网格内画出 $ \triangle A_1B_1C_1 $,使 $ \triangle A_1B_1C_1 $ 与 $ \triangle ABC $ 位似,且相似比为 $ 2:1 $;
(2)在(1)的条件下,点 $ C_1 $ 的坐标是 ______,$ \triangle A_1B_1C_1 $ 的面积是 ______ 平方单位.

(1)图略.
(2)
(1)以点 $ B $ 为位似中心,在网格内画出 $ \triangle A_1B_1C_1 $,使 $ \triangle A_1B_1C_1 $ 与 $ \triangle ABC $ 位似,且相似比为 $ 2:1 $;
(2)在(1)的条件下,点 $ C_1 $ 的坐标是 ______,$ \triangle A_1B_1C_1 $ 的面积是 ______ 平方单位.

(1)图略.
(2)
(1,0)
,10
.
答案:
(1)图略.
(2)(1,0),10.
(1)图略.
(2)(1,0),10.
6. 如图,在平面直角坐标系中,$ \triangle ABC $ 与 $ \triangle A'B'C' $ 是以点 $ P $ 为位似中心的位似图形,点 $ A $,$ B $,$ C $,$ A' $,$ B' $,$ C' $ 都在格点上.
(1)画出位似中心点 $ P $,并写出点 $ P $ 的坐标.
(2)求 $ \triangle A'B'C' $ 与 $ \triangle ABC $ 的相似比 $ k $.
(3)以点 $ P $ 为位似中心,能否再画一个 $ \triangle A_1B_1C_1 $,使它与 $ \triangle ABC $ 的相似比仍等于 $ k $?若能,请在图中画出;若不能,请说明理由.
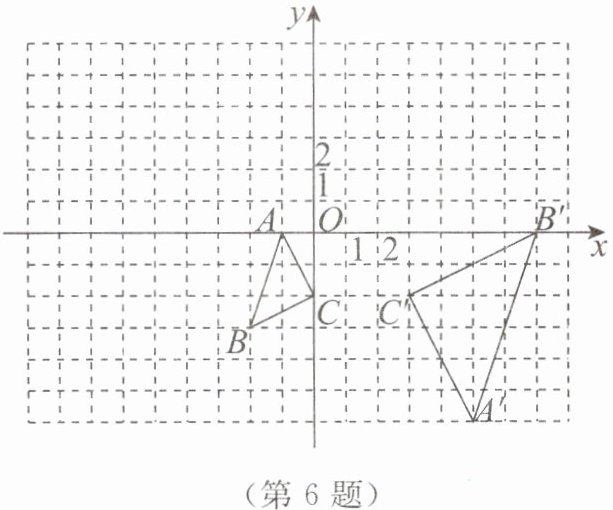
(1)画出位似中心点 $ P $,并写出点 $ P $ 的坐标.
(2)求 $ \triangle A'B'C' $ 与 $ \triangle ABC $ 的相似比 $ k $.
(3)以点 $ P $ 为位似中心,能否再画一个 $ \triangle A_1B_1C_1 $,使它与 $ \triangle ABC $ 的相似比仍等于 $ k $?若能,请在图中画出;若不能,请说明理由.

答案:
(1)图略,(1,-2).
(2)2.
(3)能,图略.
(1)图略,(1,-2).
(2)2.
(3)能,图略.
查看更多完整答案,请扫码查看


