《2025年课堂精练九年级数学上册北师大版福建专版》

1. 若两个三角形的相似比为 $1:2$,则它们的面积比为(B).
A.$1:2$
B.$1:4$
C.$2:1$
D.$4:1$

答案： B

2. 若 $\triangle ABC \backsim \triangle DEF$,且相似比为 $2:1$,则 $\triangle ABC$ 与 $\triangle DEF$ 的周长的比为(A).
A.$2:1$
B.$4:1$
C.$1:2$
D.$1:4$

答案： A

3. 两个相似三角形对应角平分线的比为 $4:3$,那么这两个三角形的面积比为(D).
A.$2:3$
B.$4:9$
C.$16:36$
D.$16:9$

答案： D

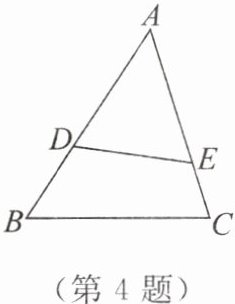
4. 如图,若 $\triangle ADE \backsim \triangle ACB$,且 $\frac{AD}{AC} = \frac{2}{3}$,四边形 $BCED$ 的面积是 $5$,则 $\triangle ADE$ 的面积是4.

答案： 4

5. 如图,在矩形 $ABDE$ 中,$AB = 3\ cm$,$BD = 7\ cm$,点 $C$ 在 $ED$ 边上,且 $EC = 1\ cm$,点 $P$ 在 $BD$ 边上移动,当以 $P$,$C$,$D$ 为顶点的三角形与 $\triangle ABP$ 相似时,求 $PD$ 的长.

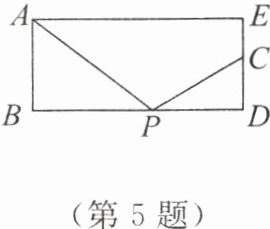
答案： $\frac{14}{5}$cm或1 cm或6 cm.

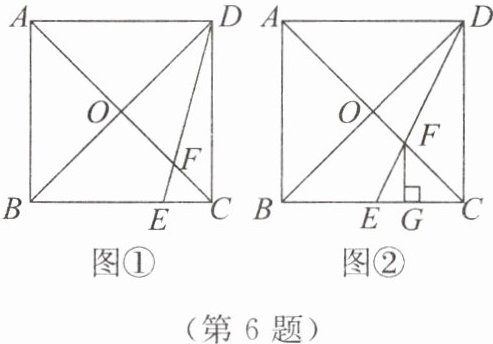
6. 如图,在正方形 $ABCD$ 中,对角线 $AC$ 与 $BD$ 相交于点 $O$,点 $E$ 是 $BC$ 上的一个动点,连接 $DE$,交 $AC$ 于点 $F$.
(1) 如图①,当 $\frac{CE}{EB} = \frac{1}{3}$ 时,求 $\frac{S_{\triangle CEF}}{S_{\triangle ADF}}$ 的值；
(2) 如图②,当点 $E$ 是 $BC$ 的中点时,过点 $F$ 作 $FG \perp BC$ 于点 $G$,求证：$CG = \frac{1}{2}BG$.

答案： 提示:
(1)$\frac{1}{16}$.
(2)先求出CF:AF,再得到CG:BG,进而说明$CG=\frac{1}{2}BG$.