《2025年实验班提优训练五年级数学上册人教版》

例1 下图中直角梯形ABCD的边BC的长是56厘米,求该梯形的面积。

解析
根据梯形的面积公式：梯形ABCD的面积= (AB+CD)×BC÷2,因为三角形ABE和三角形DCE都是等腰直角三角形,所以AB= BE,CD= CE,梯形ABCD的面积= (AB+CD)×BC÷2= BC×BC÷2。
答案：56×56÷2= 1568(平方厘米)
小结
计算时,要通过等量代换,使计算由繁到简。

答案： 解析：
根据梯形的面积公式：梯形$ABCD$的面积$S=(AB + CD) × BC÷2$。
因为$\triangle ABE$和$\triangle DCE$都是等腰直角三角形，在等腰直角三角形中，两个底角都是$45^{\circ}$，且两直角边相等，所以$AB = BE$，$CD = CE$。
那么$AB + CD=BE + CE = BC$，此时梯形$ABCD$的面积$S = BC× BC÷2$。
已知$BC = 56$厘米，将其代入公式$S = BC× BC÷2$可得：$56×56÷2 = 1568$（平方厘米）。
计算时，要通过等量代换，使计算由繁到简。
答案：
$56×56÷2 = 1568$（平方厘米）

1. 如右下图,已知两个正方形的边长分别是6 cm和8 cm,求涂色部分的面积。

答案： 8×(8+6)÷2 - 8×8÷2 = 24(cm²)
[提示]涂色部分的面积等于底是8cm、高是8 + 6 = 14(cm)的三角形的面积减去底是8cm、高是8cm的三角形的面积。

例2 如右图,在四边形ABCD中,AB= 10 dm,CD= 4 dm,∠A= 45°,∠B和∠D都是直角。求四边形ABCD的面积。

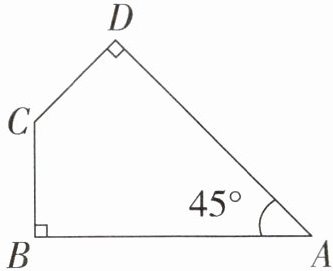
解析
观察图形可以发现,可以延长AD和BC相交于点E,得到一个大等腰直角三角形ABE和一个小等腰直角三角形ECD,如下图所示。由图可以看出,四边形ABCD的面积等于三角形ABE的面积减去三角形ECD的面积。

答案：$10×10÷2-4×4÷2= 42(dm^2)$
小结
当所求组合图形的面积不明显时,可以通过添补或者拆分的方法将图形分为若干个基本图形,再进行计算。

答案： 延长AD和BC相交于点E，形成等腰直角三角形ABE和等腰直角三角形ECD。
三角形ABE的面积：$10×10÷2=50(dm^2)$
三角形ECD的面积：$4×4÷2=8(dm^2)$
四边形ABCD的面积：$50-8=42(dm^2)$
答：四边形ABCD的面积是$42dm^2$。

2. 如右下图,三角形ABC的周长是30 cm,三角形内一点O到三角形三条边的距离都是3 cm,求三角形ABC的面积。

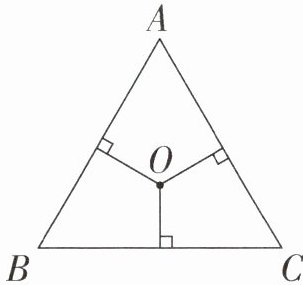
答案：
30×3÷2 = 45(cm²)
[提示]如右图，连接OA、OB、OC，得到三个高都是3cm的三角形，即三角形OAB、三角形OBC和三角形OCA，所以三角形ABC的面积 = AB×3÷2 + BC×3÷2 + AC×3÷2 = (AB + BC + AC)×3÷2 = 30×3÷2 = 45(cm²)。