第81页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 图中每个小方格的面积是$1\ \text{cm}^2$,这片叶子的面积大约是(
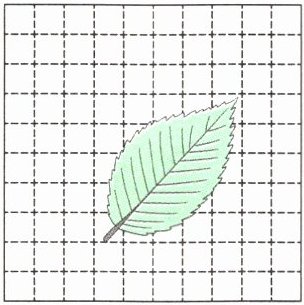
方法一:方格纸上满格的一共有(
方法二:将叶子的图形近似转化成平行四边形。$S= ah= $(
14
)$\text{cm}^2$。
方法一:方格纸上满格的一共有(
14
)格,不是满格的有(7
)格,把不满一格的按半格计算,这片叶子的面积大约是(14
)$\text{cm}^2$。方法二:将叶子的图形近似转化成平行四边形。$S= ah= $(
3×5
)$=$(15
)$\text{cm}^2$。
答案:
14 7 14 14 3×5 15(部分答案不唯一)
2. 一块地的形状近似于平行四边形,现在已测出它的底和高,如右下图。这块地的面积大约是多少平方米?(得数保留整数)


答案:
48.6×36.4≈1769(m²)[提示]根据“平行四边形的面积=底×高”计算即可。
3. 图中每个小方格的面积是$1\ \text{cm}^2$,写出涂色部分的面积。
(
(

(
28
)$\text{cm}^2$(
20
)$\text{cm}^2$
答案:
28 20 [提示]第一个图形可以近似看成一个长是7厘米、宽是4厘米的长方形,根据“长方形的面积=长×宽”计算即可。第二个图形可以近似看成一个长5厘米、宽4厘米的长方形,根据“长方形的面积=长×宽”计算即可。
4. 下面方格纸中图形的面积(涂色部分)大约是多少平方厘米?(每个小方格的面积是$1\ \text{cm}^2$)


答案:
35平方厘米[提示]利用数格子的方法解答,不满一格的都按半格计算,据此数数。或看成近似的规则图形计算,答案是近似数,不唯一。
5. 每个小方格的面积是$1\ \text{cm}^2$,下面网格中图形的面积大约是多少平方厘米?
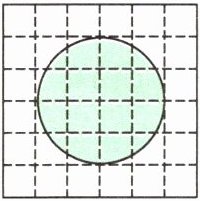

答案:
10平方厘米 [提示]利用数格子的方法解答,不满一格的都按半格计算,据此数数。
6. 每个小方格的面积是$1\ \text{cm}^2$,估计下面图中树叶的面积。
原图
图1
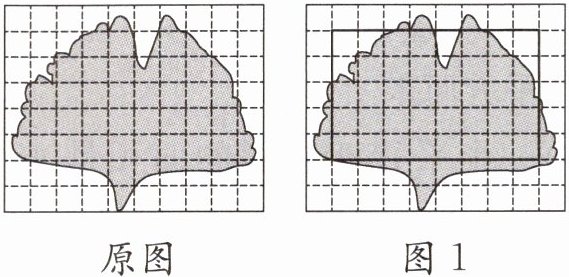
(1)用图1的方法估计树叶的面积是多少平方厘米。
(2)在原图上画一画,转化成其他一般图形或组合图形来估计树叶的面积是多少平方厘米。
原图
图1

(1)用图1的方法估计树叶的面积是多少平方厘米。
(2)在原图上画一画,转化成其他一般图形或组合图形来估计树叶的面积是多少平方厘米。
答案:
(1)8×5=40(cm²)[提示]这个不规则图形可以近似看成一个长8厘米、宽5厘米的长方形,根据“长方形的面积=长×宽”计算即可。
(2)答案不唯一,如: (4+10)×6÷2=42(cm²)[提示]这个不规则图形可以近似看成一个上底4cm、下底10cm、高6cm的梯形,根据“梯形的面积=(上底+下底)×高÷2"计算即可。
(4+10)×6÷2=42(cm²)[提示]这个不规则图形可以近似看成一个上底4cm、下底10cm、高6cm的梯形,根据“梯形的面积=(上底+下底)×高÷2"计算即可。
(1)8×5=40(cm²)[提示]这个不规则图形可以近似看成一个长8厘米、宽5厘米的长方形,根据“长方形的面积=长×宽”计算即可。
(2)答案不唯一,如:
 (4+10)×6÷2=42(cm²)[提示]这个不规则图形可以近似看成一个上底4cm、下底10cm、高6cm的梯形,根据“梯形的面积=(上底+下底)×高÷2"计算即可。
(4+10)×6÷2=42(cm²)[提示]这个不规则图形可以近似看成一个上底4cm、下底10cm、高6cm的梯形,根据“梯形的面积=(上底+下底)×高÷2"计算即可。 7. 新素养 几何直观 如右下图,平行四边形$ABCD$的面积是14平方厘米。另一个平行四边形$DEFG的边EF过点A$,点$G在边BC$上。平行四边形$DEFG$的面积是多少平方厘米?


答案:
14÷2×2=14(平方厘米)[提示]如下图,连接AG,三角形AGD的面积等于平行四边形ABCD面积的一半,三角形AGD 的面积也等于平行四边形DEFG面积的一半,所以平行四边形DEFG的面积等于平行四边形ABCD的面积。
14÷2×2=14(平方厘米)[提示]如下图,连接AG,三角形AGD的面积等于平行四边形ABCD面积的一半,三角形AGD 的面积也等于平行四边形DEFG面积的一半,所以平行四边形DEFG的面积等于平行四边形ABCD的面积。

查看更多完整答案,请扫码查看


