《2025年一遍过九年级初中数学上册人教版》

1 [2023无锡中考]给出下列命题:①各边相等的多边形是正多边形;②正多边形是中心对称图形;③正六边形的外接圆半径与边长相等;④正n边形共有n条对称轴.其中真命题的个数是( )

A.4
B.3
C.2
D.1

答案： C 各边相等、各角也相等的多边形是正多边形，只有各边相等的多边形不一定是正多边形，如菱形，故①为假命题；正三角形和正五边形不是中心对称图形，故②为假命题；正六边形中外接圆半径与边长可构成等边三角形，所以外接圆半径与边长相等，故③为真命题；根据轴对称图形的定义和正多边形的特点，可知正n边形共有n条对称轴，故④为真命题。

2 [2025福州十六中期中]若正多边形的中心角为45°,则正多边形的边数是( )

A.4
B.6
C.8
D.12

答案： C
∵正多边形的中心角为45°，
∴这个多边形的边数是360°÷45° = 8，
∴正多边形的边数是8。

3 教材P106T3变式 [2024广州海珠区期中]如图,⊙O是正方形ABCD的外接圆,若正方形ABCD的边长为4,则正方形外接圆的半径是( )

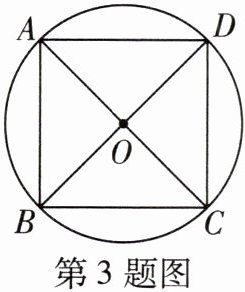
A.4
B.2
C.2√2
D.4√2

答案： C
∵正方形ABCD的边长为4，O为外心，
∴AD = 4，△OAD是等腰直角三角形，
∴OA = OD = 2√2。

4 教材P106例题变式 [2024济宁中考]如图,边长为2的正六边形ABCDEF内接于⊙O,则它的内切圆半径为( )

A.1
B.2
C.√2
D.√3

答案：
D 如图，连接OA，OB，过点O作OM⊥AB，垂足为点M，
∵六边形ABCDEF是正六边形，点O是它的中心，
∴∠AOB = 360°/6 = 60°。
∵OA = OB，
∴△AOB是等边三角形，
∵OM⊥AB，
∴AM = BM = 1/2AB = 1。在Rt△AOM中，OA = 2，AM = 1，
∴OM = √(OA² - AM²) = √3，即它的内切圆半径为√3。

5 新趋势·数学文化 [2025石家庄四十二中月考]刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来估算圆周率,开创了中国数学发展史上圆周率研究的新纪元.某同学在学习“割圆术”的过程中,作了一个如图所示的圆内接正十二边形.若⊙O的半径为2,则这个圆内接正十二边形的面积为( )

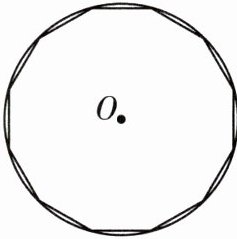
A.3
B.12
C.4π
D.12π

答案：
B 如图，过点A作AC⊥OB于点C，
∵圆的内接正十二边形的中心角为360°÷12 = 30°，
∴∠AOB = 30°。
∵OA = 2，
∴AC = 1/2OA = 1，
∴S△AOB = 1/2AC·OB = 1，
∴这个圆的内接正十二边形的面积为12×1 = 12。

6 [2024广元中考]点F是正五边形ABCDE边DE的中点,连接BF并延长,与CD延长线交于点G,则∠BGC的度数为______.

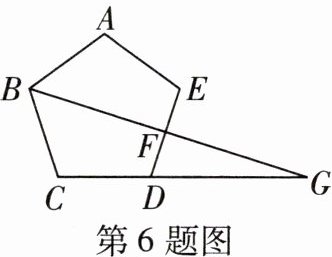
答案： 18° 由正五边形的性质可知，BG是正五边形ABCDE的对称轴，
∴∠DFG = 90°。
∵∠FDG是正五边形ABCDE的外角，
∴∠FDG = 360°÷5 = 72°，
∴∠BGC = 90° - 72° = 18°。

7 [2024南京鼓楼区期中]如图,点A,B,C,D为一个正多边形的顶点,点O为正多边形的中心,若∠ADB= 18°,则这个正多边形的边数为______.

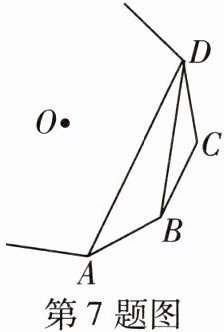
答案：
10 如图，作正多边形的外接圆，连接AO，BO，
∴∠AOB = 2∠ADB = 36°，
∴这个正多边形的边数为360°/36° = 10。

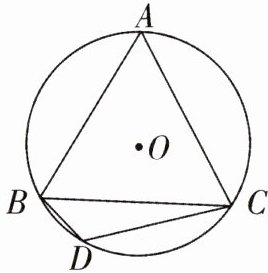
8 如图,等边三角形ABC内接于⊙O,BD为内接正十二边形的一边,CD= 5√2,求⊙O的半径.

答案：
解：设⊙O的半径为r。如图，连接OB，OC，OD。则∠BOC = 360°/3 = 120°，∠BOD = 360°/12 = 30°，
∴∠COD = ∠BOC - ∠BOD = 120° - 30° = 90°。在Rt△COD中，根据勾股定理，得r² + r² = (5√2)²，
∴r = 5。故⊙O的半径为5。

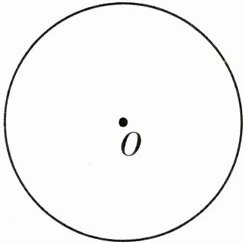
9 如图,已知⊙O的半径为1 cm,求作⊙O的内接正八边形.

答案：
解：
(1)如图，作直径AC。
(2)作AC的垂直平分线BD交⊙O于B，D两点。
(3)连接AD，作AD的垂直平分线交⌢AD于点M，则M为⌢AD的中点。
(4)以点A为圆心，AM的长为半径作弧交圆O于点E，用同样的方法作出点F，G。
(5)依次连接各点，即得⊙O的内接正八边形。正八边形AEBFCGDM即为所求作的⊙O的内接正八边形。