第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1 如图,已知$\triangle AOB$,将$\triangle AOB绕点A逆时针旋转\alpha (0^{\circ }<\alpha <180^{\circ })$后,得到$\triangle AED$,连接$BD$.
【基础设问】
(1)如图1,若$\angle OAB= 30^{\circ }$,$\angle EAB= 120^{\circ }$,则$\alpha =$____.
(2)在(1)的条件下,若$AB= 1$,则$BD= $____.
【能力设问】
(3)如图2,$\alpha =60^{\circ }$,连接$OE$.
①求证:$\triangle AOE$是等边三角形.
②连接$OD$,若$\angle AOB= 150^{\circ }$,$\angle AOD= 105^{\circ }$,试判断$\triangle EOD$的形状,并说明理由.
【拓展设问】
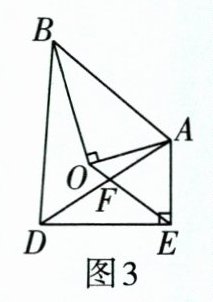
(4)如图3,若$\angle AOB= 90^{\circ }$,连接$OE交AD于点F$.
①求证:$\angle AOE= \angle ADB$.
②设$\angle ABO= \beta $,则当$\alpha$,$\beta$满足什么条件时,$\triangle DEF$是等腰三角形?


【基础设问】
(1)如图1,若$\angle OAB= 30^{\circ }$,$\angle EAB= 120^{\circ }$,则$\alpha =$____.
(2)在(1)的条件下,若$AB= 1$,则$BD= $____.
【能力设问】
(3)如图2,$\alpha =60^{\circ }$,连接$OE$.
①求证:$\triangle AOE$是等边三角形.
②连接$OD$,若$\angle AOB= 150^{\circ }$,$\angle AOD= 105^{\circ }$,试判断$\triangle EOD$的形状,并说明理由.
【拓展设问】
(4)如图3,若$\angle AOB= 90^{\circ }$,连接$OE交AD于点F$.
①求证:$\angle AOE= \angle ADB$.
②设$\angle ABO= \beta $,则当$\alpha$,$\beta$满足什么条件时,$\triangle DEF$是等腰三角形?



答案:
(1)解:90°
∵ 将△AOB 旋转得到△AED,
∴ ∠DAE = ∠OAB = 30°,
又∠EAB = 120°,
∴ α = ∠DAB = 120° - 30° = 90°.
(2)解:$\sqrt{2}$
由旋转的性质,知 AB = AD.
∵ ∠DAB = 90°,
∴ BD = $\sqrt{AB^2 + AD^2} = \sqrt{2}$.
(3)①证明:
∵ 将△AOB 绕点 A 逆时针旋转 60°后,得到△AED,
∴ △AOB≌△AED,∠OAE = 60°,
∴ AO = AE,
∴ △AOE 是等边三角形.
②解:△EOD 为等腰直角三角形.理由如下:
由①知△AOE 是等边三角形,
∴ ∠AEO = ∠AOE = 60°.
由旋转的性质,知∠AED = ∠AOB = 150°,
∴ ∠OED = 150° - 60° = 90°.
∵ ∠AOD = 105°,
∴ ∠EOD = 105° - 60° = 45°,
∴ △EOD 是等腰直角三角形.
(4)①证明:
∵ 将△AOB 绕点 A 逆时针旋转 α 后,得到△AED,
∴ AE = AO,AD = AB,∠BAD = ∠EAO = α,
∴ ∠AOE = ∠AEO = $\frac{1}{2}(180° - ∠EAO) = 90° - \frac{α}{2}$,∠ADB = $\frac{1}{2}(180° - ∠BAD) = 90° - \frac{α}{2}$,
∴ ∠AOE = ∠ADB.
②解:
∵ ∠ABO = β,
∴ ∠ADE = β.
△DEF 是等腰三角形分三种情况讨论:
当 DF = EF 时,∠ADE = ∠DEF = β.
∵ ∠AED = ∠AEO + ∠DEF,
∴ 90° = $90° - \frac{α}{2} + β$,
∴ β = $\frac{α}{2}$.
当 DE = DF 时,∠DEF = $\frac{1}{2}(180° - ∠ADE) = 90° - \frac{β}{2}$,
∵ ∠AED = ∠AEO + ∠DEF,
∴ $90° - \frac{α}{2} + 90° - \frac{β}{2} = 90°$,
∴ α + β = 180°.
当 DE = EF 时,点 F 在 DA 的延长线上,不符合题意,舍去.
综上,当 β = $\frac{α}{2}$ 或 α + β = 180°时,△DEF 是等腰三角形.
(1)解:90°
∵ 将△AOB 旋转得到△AED,
∴ ∠DAE = ∠OAB = 30°,
又∠EAB = 120°,
∴ α = ∠DAB = 120° - 30° = 90°.
(2)解:$\sqrt{2}$
由旋转的性质,知 AB = AD.
∵ ∠DAB = 90°,
∴ BD = $\sqrt{AB^2 + AD^2} = \sqrt{2}$.
(3)①证明:
∵ 将△AOB 绕点 A 逆时针旋转 60°后,得到△AED,
∴ △AOB≌△AED,∠OAE = 60°,
∴ AO = AE,
∴ △AOE 是等边三角形.
②解:△EOD 为等腰直角三角形.理由如下:
由①知△AOE 是等边三角形,
∴ ∠AEO = ∠AOE = 60°.
由旋转的性质,知∠AED = ∠AOB = 150°,
∴ ∠OED = 150° - 60° = 90°.
∵ ∠AOD = 105°,
∴ ∠EOD = 105° - 60° = 45°,
∴ △EOD 是等腰直角三角形.
(4)①证明:
∵ 将△AOB 绕点 A 逆时针旋转 α 后,得到△AED,
∴ AE = AO,AD = AB,∠BAD = ∠EAO = α,
∴ ∠AOE = ∠AEO = $\frac{1}{2}(180° - ∠EAO) = 90° - \frac{α}{2}$,∠ADB = $\frac{1}{2}(180° - ∠BAD) = 90° - \frac{α}{2}$,
∴ ∠AOE = ∠ADB.
②解:
∵ ∠ABO = β,
∴ ∠ADE = β.
△DEF 是等腰三角形分三种情况讨论:
当 DF = EF 时,∠ADE = ∠DEF = β.
∵ ∠AED = ∠AEO + ∠DEF,
∴ 90° = $90° - \frac{α}{2} + β$,
∴ β = $\frac{α}{2}$.
当 DE = DF 时,∠DEF = $\frac{1}{2}(180° - ∠ADE) = 90° - \frac{β}{2}$,
∵ ∠AED = ∠AEO + ∠DEF,
∴ $90° - \frac{α}{2} + 90° - \frac{β}{2} = 90°$,
∴ α + β = 180°.
当 DE = EF 时,点 F 在 DA 的延长线上,不符合题意,舍去.
综上,当 β = $\frac{α}{2}$ 或 α + β = 180°时,△DEF 是等腰三角形.
2 如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,$\triangle ABC$的顶点都在格点上.
【基础设问】
(1)画出将$\triangle ABC$向左平移4个单位长度得到的$\triangle A_{1}B_{1}C_{1}$.
(2)画出$\triangle ABC关于原点成中心对称的\triangle A_{2}B_{2}C_{2}$.
【能力设问】
(3)若将$\triangle A_{1}B_{1}C_{1}绕某一点经过一次旋转得到\triangle A_{2}B_{2}C_{2}$,则旋转中心的坐标为____,旋转角的度数为____.
(4)$\triangle A_{1}B_{1}C_{1}中A_{1}C_{1}边上的一点P_{1}(m,n)在\triangle A_{2}B_{2}C_{2}中A_{2}C_{2}边上的对应点P_{2}$的坐标为____.
(5)画出将$\triangle A_{2}B_{2}C_{2}绕点B_{2}逆时针旋转90^{\circ }得到的\triangle A_{3}B_{2}C_{3}$.

【基础设问】
(1)画出将$\triangle ABC$向左平移4个单位长度得到的$\triangle A_{1}B_{1}C_{1}$.
(2)画出$\triangle ABC关于原点成中心对称的\triangle A_{2}B_{2}C_{2}$.
【能力设问】
(3)若将$\triangle A_{1}B_{1}C_{1}绕某一点经过一次旋转得到\triangle A_{2}B_{2}C_{2}$,则旋转中心的坐标为____,旋转角的度数为____.
(4)$\triangle A_{1}B_{1}C_{1}中A_{1}C_{1}边上的一点P_{1}(m,n)在\triangle A_{2}B_{2}C_{2}中A_{2}C_{2}边上的对应点P_{2}$的坐标为____.
(5)画出将$\triangle A_{2}B_{2}C_{2}绕点B_{2}逆时针旋转90^{\circ }得到的\triangle A_{3}B_{2}C_{3}$.

答案:
解:
(1)△A₁B₁C₁ 如图所示.

(2)△A₂B₂C₂ 如图所示.
(3)(-2,0) 180°
(4)(-4 - m,-n)
(5)△A₃B₂C₃ 如图所示.
解:
(1)△A₁B₁C₁ 如图所示.

(2)△A₂B₂C₂ 如图所示.
(3)(-2,0) 180°
(4)(-4 - m,-n)
(5)△A₃B₂C₃ 如图所示.
查看更多完整答案,请扫码查看


