《2025年一遍过九年级初中数学上册人教版》

1 [2024厦门集美区期中改编]如图1,正方形$ABCD与正方形AEFG的边AB$,$AE(AB ＜ AE)$在同一条直线上,正方形$AEFG以点A$为旋转中心逆时针旋转,设旋转角为$\alpha$.在旋转过程中,两个正方形只有点$A$重合,其他顶点均不重合,连接$BE$,$DG$.
(1)当正方形$AEFG$旋转至如图2所示的位置时,求证：$BE = DG$.
(2)延长$GD交AE于点M$,交$BE于点N$,求证：$GN \perp BE$.

答案： 证明:
(1)由旋转的性质可知∠BAE=∠DAG,由正方形的性质可知AB=AD,AE=AG.
∵在△ABE和△ADG中，{AB=AD,∠BAE=∠DAG,AE=AG}
∴△ABE≌△ADG(SAS),
∴BE=DG;
(2)由
(1)知△ABE≌△ADG,
∴∠AGD=∠AEB.
∵∠AMG=∠EMN,
∴∠GAM=∠ENM=90°(8字模型),
∴GN⊥BE;

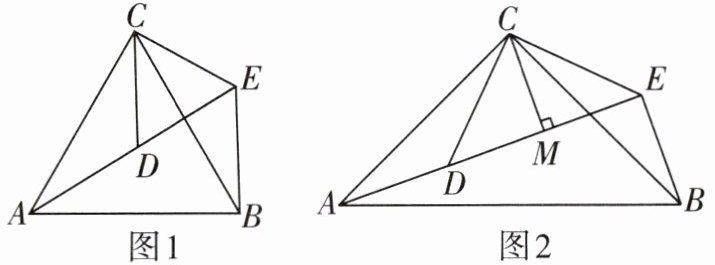
2 [2025贵港桂平期中](1)如图1,$\triangle ACB和\triangle DCE$均为等边三角形,当点$A$,$D$,$E$在同一条直线上时,连接$BE$.
填空：①$\angle AEB$的度数为____；②线段$AD$,$BE$之间的数量关系为____.
(2)如图2,$\triangle ACB和\triangle DCE$均为等腰三角形,$\angle ACB = \angle DCE = 90^{\circ}$,$A$,$D$,$E$三点在同一条直线上,$CM为\triangle DCE中DE$边上的高,连接$BE$,请判断$\angle AEB的度数及线段CM$,$AE$,$BE$之间的数量关系,并说明理由.
(3)如图1中的$\triangle ACB和\triangle DCE$,将$\triangle DCE绕点C$旋转,在旋转的过程中,当点$A$,$D$,$E$不在同一条直线上时,设直线$AD与BE相交于点O$,旋转角为$\theta(0^{\circ} ＜ \theta ＜ 180^{\circ})$,尝试在图中探索$\angle AOE$的度数,直接写出结果,不必说明理由.

答案：
解:
(1)①60° ②AD=BE
①
∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE,
∴∠ADC=∠BEC;
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°,
∵点A,D,E在同一直线上,
∴∠ADC=120°,
∴∠BEC=120°,
∴∠AEB=∠BEC−∠CED=60°.
②
∵△ACD≌△BCE,
∴AD=BE.
(2)∠AEB=90°,AE=BE+2CM.理由如下:
∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,
∴CA=CB,CD=CE,∠ACD=∠BCE,
∴△ACD≌△BCE,
∴BE=AD,∠ADC=∠BEC.
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°.
∵A,D,E三点在同一条直线上,
∴∠ADC=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC−∠CED=90°.
∵△DCE为等腰直角三角形,CM为△DCE中DE边上的高,
∴CM为Rt△DCE的斜边DE上的中线,
∴CM=$\frac{1}{2}$DE,
∴AE=AD+DE=BE+2CM.
(3)60°或120°.
∵旋转角为θ(0°＜θ＜180°),
∴按点E在AD上方和下方两种情况进行分析.如图1,由
(1)知△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠CAB=∠CBA=60°,
∴∠OAB+∠OBA=120°,
∴∠AOE=180°−120°=60°.如图2,同理求得∠AOB=60°,
∴∠AOE=120°.综上,∠AOE的度数是60°或120°.