《2025年一遍过九年级初中数学上册人教版》

10 [2022温州中考]已知点$A(a,2),B(b,2),C(c,7)都在抛物线y= (x-1)^{2}-2$上,点$A在点B$左侧,下列选项正确的是 ( )

A.若$c＜0$,则$a＜c＜b$
B.若$c＜0$,则$a＜b＜c$
C.若$c＞0$,则$a＜c＜b$
D.若$c＞0$,则$a＜b＜c$

答案： D 由题意可知,抛物线$y=(x-1)^{2}-2$的对称轴为直线$x=1$,开口向上,当$x＞1$时,y随x的增大而增大,当$x＜1$时,y随x的增大而减小.$\because$点$A(a,2)$,$B(b,2)$,$C(c,7)$都在抛物线$y=(x-1)^{2}-2$上,点A在点B左侧,$\therefore$若$c＜0$,则$c＜a＜b$,故选项A,B均不符合题意;若$c＞0$,则$a＜b＜c$,故选项C不符合题意,选项D符合题意.

11 [2024长春五十二中期中]如图,在平面直角坐标系中,点$A是抛物线y= -(x-h)^{2}+5$上的任意一点,过点$A作AB// x轴交抛物线于点B$,若$AB= 4$,则点$B到x$轴的距离为 ( )

A.1
B.2
C.3
D.4

答案： A $\because AB// x$轴,$y=-(x-h)^{2}+5$,$\therefore$A,B关于直线$x=h$对称(令点A在对称轴的左侧),$\therefore y_{A}=y_{B}$.$\because AB=4$,$\therefore x_{A}=h-\frac{4}{2}=h-2$,$\therefore y_{A}=-(h-2-h)^{2}+5=-4+5=1$,$\therefore y_{B}=y_{A}=1$,$\therefore$点B到x轴的距离为1.

12 已知抛物线$y= a(x-h)^{2}+k与x轴有两个交点A(-1,0),B(3,0)$,抛物线$y= a(x-h-m)^{2}+k与x轴的一个交点是(4,0)$,则$m$的值是 ( )

A.5
B.-1
C.5或1
D.-5或-1

答案： C $\because$抛物线$y=a(x-h)^{2}+k$的对称轴为直线$x=h$,抛物线$y=a(x-h-m)^{2}+k$的对称轴为直线$x=h+m$,$\therefore$当点$A(-1,0)$平移后的对应点为(4,0)时,$m=4-(-1)=5$;当点$B(3,0)$平移后的对应点为(4,0)时,$m=4-3=1$.综上可得,m的值为5或1.

13 [2025南京金陵汇文学校月考]已知关于$x的二次函数y= 2(x-1)^{2}+3$,当$-1＜x＜2$时,函数值$y$的取值范围为____.

答案： $3\leqslant y＜11$ 由二次函数$y=2(x-1)^{2}+3$可知,对称轴为直线$x=1$.$\because 2＞0$,$\therefore$当$x=1$时,二次函数$y=2(x-1)^{2}+3$有最小值3,由$|-1-1|＞|2-1|$,根据距离对称轴越远,函数值越大,且当$x=-1$时,$y=11$,可知当$-1＜x＜2$时,函数值y的取值范围为$3\leqslant y＜11$.

14 如图,已知二次函数$y= -3(x+m)^{2}+k(m,k$为常数,且$k＞0)的图象与x轴交于A,B$两点,若$AB= 2$,则$k$的值是____.

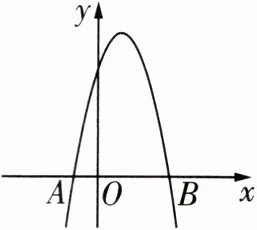
答案：
3 如图,设抛物线的顶点为C,将抛物线向左平移,使顶点C落在y轴上的点$C'$处,点A,B的对应点分别为$A'$,$B'$,设平移后的二次函数的解析式为$y=-3x^{2}+k$,$\because AB=2$,$\therefore A'B'=2$,$\therefore OB'=1$,即点$B'$的坐标为(1,0),把点$B'$的坐标代入$y=-3x^{2}+k$,得$0=-3×1^{2}+k$,$\therefore k=3$.

15 [新趋势·代数推理][2025厦门双十中学期中]在平面直角坐标系中,设二次函数$y= -\frac {1}{2}(x-2m)^{2}+3-m(m$是实数).
(1)当$m= 2$时,若点$A(8,n)$在该函数图象上,求$n$的值.
(2)小明说二次函数图象的顶点在直线$y= -\frac {1}{2}x+3$上,你认为他的说法对吗? 为什么?
(3)已知点$P(a+1,c),Q(4m-5+a,c)$都在该二次函数的图象上. 求证:$c≤\frac {13}{8}$.

答案：
(1)解:当$m=2$时,$y=-\frac{1}{2}(x-2×2)^{2}+3-2=-\frac{1}{2}(x-4)^{2}+1$,
$\because$点$A(8,n)$在该函数图象上,
$\therefore -\frac{1}{2}×(8-4)^{2}+1=n$,即$n=-7$.
(2)解:小明的说法对.理由如下:
$\because y=-\frac{1}{2}(x-2m)^{2}+3-m$,$\therefore$二次函数图象的顶点为$(2m,3-m)$,
当$x=2m$时,$-\frac{1}{2}x+3=-\frac{1}{2}×2m+3=-m+3$,
$\therefore$顶点$(2m,3-m)$在直线$y=-\frac{1}{2}x+3$上.
(3)证明:$\because$点$P(a+1,c)$,$Q(4m-5+a,c)$都在该二次函数的图象上,
$\therefore$二次函数图象的对称轴为直线$x=\frac{a+1+4m-5+a}{2}=a+2m-2$.(点P,Q的纵坐标相等,则点P,Q两点关于抛物线的对称轴对称)
由题意可得,二次函数图象的顶点为$(2m,3-m)$,
$\therefore a+2m-2=2m$,$\therefore a=2$,$\therefore P(3,c)$,
$\therefore c=-\frac{1}{2}×(3-2m)^{2}+3-m=-2m^{2}+5m-\frac{3}{2}=-2(m-\frac{5}{4})^{2}+\frac{13}{8}$.
$\because (m-\frac{5}{4})^{2}\geqslant0$,$\therefore -2(m-\frac{5}{4})^{2}\leqslant0$,
$\therefore c=-2(m-\frac{5}{4})^{2}+\frac{13}{8}\leqslant\frac{13}{8}$.

16 [推理能力][2022丽水中考]如图,已知点$M(x_{1},y_{1}),N(x_{2},y_{2})在二次函数y= a(x-2)^{2}-1(a＞0)$的图象上,且$x_{2}-x_{1}= 3$.
(1)若二次函数的图象经过点$(3,1)$.
①求这个二次函数的解析式;
②若$y_{1}= y_{2}$,求顶点到$MN$的距离.
(2)当$x_{1}≤x≤x_{2}$时,二次函数的最大值与最小值的差为1,点$M,N$在对称轴的异侧,求$a$的取值范围.

答案： 解:
(1)①$\because$二次函数$y=a(x-2)^{2}-1(a＞0)$的图象经过点(3,1),$\therefore 1=a-1$,$\therefore a=2$,
$\therefore$二次函数的解析式为$y=2(x-2)^{2}-1$.
②$\because y_{1}=y_{2}$,$\therefore$点M,N关于抛物线的对称轴对称.
$\because$抛物线的对称轴是直线$x=2$,且$x_{2}-x_{1}=3$,
$\therefore x_{1}=\frac{1}{2}$,$x_{2}=\frac{7}{2}$.
当$x_{1}=\frac{1}{2}$时,$y_{1}=2×(\frac{1}{2}-2)^{2}-1=\frac{7}{2}$,
$\therefore$当$y_{1}=y_{2}$时,顶点到MN的距离为$\frac{7}{2}+1=\frac{9}{2}$.
(2)已知点M,N在对称轴的异侧,对称轴为直线$x=2$.
若$y_{1}\geqslant y_{2}$,则$x_{2}＞2$,且$\frac{x_{1}+x_{2}}{2}\leqslant2$.
$\because x_{2}-x_{1}=3$,$\therefore -1＜x_{1}\leqslant\frac{1}{2}$.
$\because$函数的最大值为$y_{1}=a(x_{1}-2)^{2}-1$,最小值为-1,
$\therefore y_{1}-(-1)=1$,$\therefore a=\frac{1}{(x_{1}-2)^{2}}$.
$\because \frac{9}{4}\leqslant(x_{1}-2)^{2}＜9$,$\therefore \frac{1}{9}＜a\leqslant\frac{4}{9}$;
若$y_{1}\leqslant y_{2}$,则$x_{1}＜2$,且$\frac{x_{1}+x_{2}}{2}\geqslant2$.
$\because x_{2}-x_{1}=3$,$\therefore \frac{1}{2}\leqslant x_{1}＜2$.
$\because$函数的最大值为$y_{2}=a(x_{2}-2)^{2}-1$,最小值为-1,
$\therefore y_{2}-(-1)=1$,$\therefore a=\frac{1}{(x_{2}-2)^{2}}=\frac{1}{(x_{1}+1)^{2}}$.
$\because \frac{9}{4}\leqslant(x_{1}+1)^{2}＜9$,$\therefore \frac{1}{9}＜a\leqslant\frac{4}{9}$.
综上所述,$\frac{1}{9}＜a\leqslant\frac{4}{9}$.