《2025年一遍过九年级初中数学上册人教版》

1 跨学科·语文“海日生残夜,江春入旧年.”如图是诗句所描绘的日出美景,图中太阳与海天交界处可看成圆与直线,它们的位置关系是( )


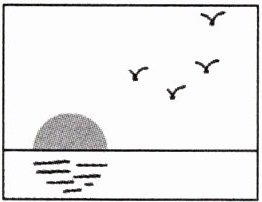
A.相切
B.相交
C.相离
D.平行

答案： B

2 [2025扬州江都区期中]$\odot O$的半径为2,圆心O到直线l的距离为3,则直线l与$\odot O$( )

A.相离
B.相切
C.相交
D.相切或相交

答案： A
∵⊙O的半径为2,圆心O到直线l的距离为3,3＞2,
∴直线l与⊙O相离.

3 已知$\odot O$的半径等于5,点P在直线l上,圆心O到点P的距离为5,那么直线l与$\odot O$的位置关系是( )

A.相切
B.相交
C.相切或相离
D.相交或相切

答案： D
∵⊙O的半径为5,OP=5,
∴点O到直线l的距离d≤5,
∴直线l与⊙O的位置关系是相交或相切.

4 [2024清华附中上地学校月考]如图,在$\triangle ABC$中,$AB= AC$,AD是$\triangle ABC$的角平分线.以点A为圆心,AD长为半径作$\odot A$,则$\odot A$与BC的位置关系是( )

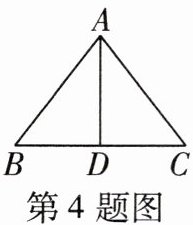
A.相交
B.相切
C.相离


D.不确定

答案： B
∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,
∴点A到BC的距离等于AD的长.
∵以点A为圆心,AD长为半径作⊙A,
∴⊙A与BC相切.

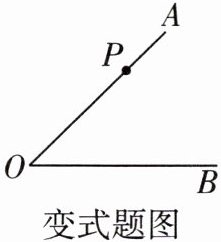
变式 如图,P为$∠AOB$边OA上一点,$∠AOB= 45^{\circ }$,$OP= 4cm$,以P为圆心,2cm长为半径的圆与OB的位置关系是( )

A.相离
B.相交
C.相切
D.无法确定

答案： A 如图,过点P作PD⊥OB于点D.
∵∠AOB=45°,
∴PD=OD.在Rt△ODP中,OP²=OD²+PD²=2PD²,OP=4cm,
∴PD=√2/2×4=2√2(cm).
∵2√2＞2,
∴以P为圆心,2cm长为半径的圆与OB的位置关系是相离.

5 [2025武汉江汉区期中]在平面直角坐标系中,点P的坐标为$(3,-4)$,以P为圆心,4个单位长度为半径作圆,下列说法正确的是( )

A.原点O在$\odot P$内
B.原点O在$\odot P$上
C.$\odot P$与x轴相切,与y轴相交
D.$\odot P$与y轴相切,与x轴相交

答案： C
∵点P的坐标为(3,-4),
∴点P到x轴的距离为4,到y轴的距离为3,到原点的距离为√(3²+4²)=5.
∵以P为圆心,4个单位长度为半径作圆,
∴原点O在⊙P外,⊙P与x轴相切,与y轴相交,故选项A,B,D不符合题意,选项C符合题意.

变式 在平面直角坐标系中,已知点$A(3,4)$,如果$\odot A$与两坐标轴有且只有3个公共点,那么$\odot A的半径r= $( )

A.3
B.4
C.3或4
D.4或5

答案： D 如图,①当⊙A与x轴相切时,r=4,此时⊙A与坐标轴有且只有3个公共点.②当⊙A经过原点时,r=5,此时⊙A与坐标轴有且只有3个公共点.

6 [2025重庆渝北区期中]已知$\odot A$的半径为r,圆心A到直线m的距离为d,若d,r是方程$x^{2}-7x+12= 0$的两个根,则直线m和$\odot A$的位置关系是( )

A.相切
B.相离
C.相交
D.相离或相交

答案： D 解方程x²-7x+12=0,得x₁=3,x₂=4.当d=3,r=4时,直线m和⊙A相交;当d=4,r=3时,直线m和⊙A相离.

7 教材P101T2变式 已知$Rt\triangle ABC的斜边AB= 6$,直角边$AC= 3$,以点C为圆心作$\odot C$.
(1)当半径r为多少时,直线AB与$\odot C$相切？
(2)当$\odot C$与线段AB只有一个公共点时,求半径r的取值范围.
(3)当$\odot C$与线段AB没有公共点时,求半径r的取值范围.

答案：
(1)如图,过点C作CD⊥AB于点D,在Rt△ACB中,由勾股定理,得BC=√(AB²-AC²)=√(6²-3²)=3√3.
∵1/2CD·AB=1/2AC·BC,
∴CD=(3×3√3)/6=3√3/2,
∴当r=3√3/2时,直线AB与⊙C相切.
(2)当r=3√3/2或3＜r≤3√3时,⊙C与线段AB只有一个公共点.
(3)当0＜r＜3√3/2或r＞3√3时,⊙C与线段AB没有公共点.