《2025年一遍过九年级初中数学上册人教版》

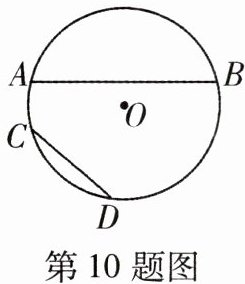
10 一题多解易错题[2025鞍山千山区期中]如图,$\overset{\frown}{AB}$,$\overset{\frown}{CD}是\odot O$的两段弧,且$\overset{\frown}{AB}= 2\overset{\frown}{CD}$,则弦AB与CD之间的关系为 ( )

A.$AB= 2CD$
B.$AB＜2CD$
C.$AB＞2CD$
D.不能确定

答案：
B 解法一 如图,在圆上截取$\widehat{DE}=\widehat{CD}$,连接DE,CE,则有$\widehat{CE}=2\widehat{CD}$,CD=DE.
∵$\widehat{AB}=2\widehat{CD}$,
∴$\widehat{AB}=\widehat{CE}$,
∴AB=CE.
∵2CD=CD+DE＞CE(点拨:三角形任意两边之和大于第三边),
∴AB＜2CD.
解法二 取$\widehat{AB}$的中点E,连接AE,BE,则$\widehat{AB}=2\widehat{AE}=2\widehat{BE}$.
∵$\widehat{AB}=2\widehat{CD}$,
∴$\widehat{AE}=\widehat{BE}=\widehat{CD}$,
∴AE=BE=CD.在△ABE中,AB＜AE+BE,即AB＜2CD.
易错分析 本题的易错之处是由$\widehat{AB}=2\widehat{CD}$直接得到AB=2CD.在同圆或等圆中,由弧相等可推出相应的弦相等,但当弧有倍数关系时,弦没有相应的倍数关系.

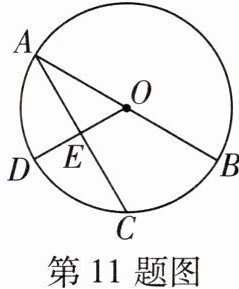
11 [2025江苏启东中学月考]如图,AB是$\odot O$的直径,$\angle BOD= 120^{\circ}$,点C为弧BD的中点,AC交OD于点E,$DE= 1$,则AE的长为 ( )

A.$2\sqrt{5}$
B.$\sqrt{5}$
C.$2\sqrt{3}$
D.$\sqrt{3}$

答案：
D 如图,连接OC.
∵∠DOB=120°,
∴∠AOD=60°.
∵$\widehat{CD}=\widehat{BC}$,
∴∠DOC=∠BOC=60°,
∴$\widehat{AD}=\widehat{CD}$,
∴OD⊥AC,
∴∠OAE=30°,设OA=r,则OE=$\frac{1}{2}$r=DE=1,
∴OA=2,
∴AE=$\sqrt{OA^2-OE^2}=\sqrt{3}$.

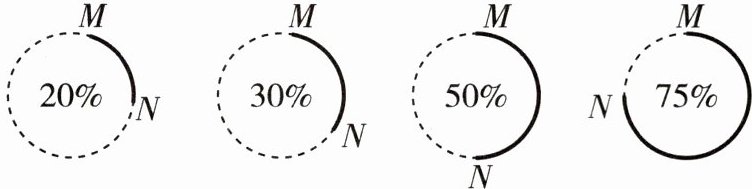
12 新考法[2025北京育才学校期中]计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.如图是同一个任务进行到不同阶段时进度条的示意图,当任务完成的百分比为x时,线段MN的长度记为$d(x)$.下列描述正确的是 ( )

A.当$x_{1}＜x_{2}$时,$d(x_{1})＜d(x_{2})$
B.当$d(x_{1})＜d(x_{2})$时,$x_{1}＜x_{2}$
C.当$x_{1}= 2x_{2}$时,$d(x_{1})= 2d(x_{2})$
D.当$x_{1}+x_{2}= 1$时,$d(x_{1})= d(x_{2})$

答案： D 当$x_1$=20%,$x_2$=80%时,d($x_1$)=d($x_2$),故A项错误;当$x_1$=80%,$x_2$=50%时,满足d($x_1$)＜d($x_2$),但$x_1$＞$x_2$,故B项错误;当$x_1$=100%,$x_2$=50%时,满足$x_1$=2$x_2$,但d($x_1$)=0,d($x_2$)=直径,d($x_1$)≠2d($x_2$),故C项错误;当$x_1$+$x_2$=1时,此时线段MN的长度是一样的,故d($x_1$)=d($x_2$),故D项正确.

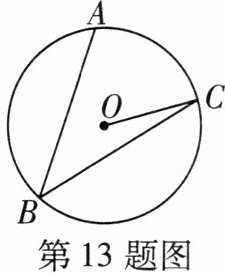
13 如图,点A,B,C在$\odot O$上,分别连接AB,BC,OC.若$AB= BC$,$\angle B= 40^{\circ}$,则$\angle OCB$的度数为______.

答案：
20°

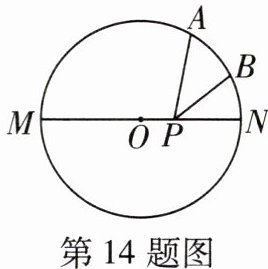
14 如图,A是半圆MN的三等分点,B是$\overset{\frown}{AN}$的中点,P是直径MN上一动点,$\odot O$的半径为1,则$AP+BP$的最小值为______.

答案：
$\sqrt{2}$ 如图,作点A关于MN的对称点A',根据圆的对称性,得点A'必在圆上,连接BA'交MN于点P',则此时PA+PB的值最小,此时P'A+P'B=P'A'+P'B=A'B.连接OA',OB,OA.
∵$\widehat{AN}=\frac{1}{3}\widehat{MN}$,
∴∠A'ON=∠AON=60°.
∵$\widehat{AB}=\widehat{BN}$,
∴∠BON=$\frac{1}{2}$∠AON=30°,
∴∠A'OB=90°.
∴在Rt△A'OB中,A'B=$\sqrt{OA'^2+OB^2}=\sqrt{2}$,即AP+BP的最小值是$\sqrt{2}$.

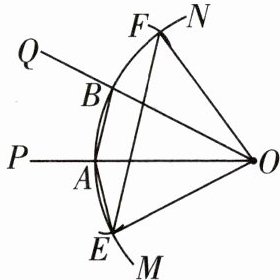
15 如图,已知锐角$\angle POQ$,在射线OP上取一点A,以点O为圆心,OA长为半径作$\overset{\frown}{MN}$,交射线OQ于点B,连接AB,分别以点A,B为圆心,AB长为半径作弧,交$\overset{\frown}{MN}$于点E,F,连接OE,EF,EA,OF.
(1)求证:$\angle EAO= \angle BAO$.
(2)若$OE= EF$,求$\angle POQ$的度数.

答案：
(1)证明：由题意得，OA=OE=OB，AE=AB。
在△ABO和△AEO中，
$\left\{\begin{array}{l} AB=AE\\ AO=AO\\ OB=OE\end{array}\right.$
∴△ABO≌△AEO(SSS)。
∴∠EAO=∠BAO。
(2)解：由题意得，BF=AB，同理可证∠FBO=∠ABO。
设∠POQ=α，则∠AOE=∠AOB=α，∠BOF=∠AOB=α，
∴∠EOF=∠AOE+∠AOB+∠BOF=3α。
∵OE=OF，OE=EF，
∴OE=OF=EF。
∴△OEF是等边三角形。
∴∠EOF=60°。
∴3α=60°，α=20°。
即∠POQ的度数为20°。

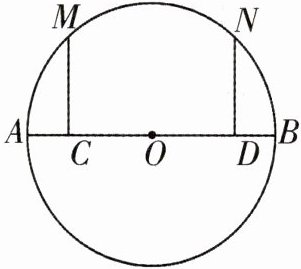
16 推理能力如图,在$\odot O$中,C,D是直径AB上的两点,且$AC= BD$,$MC\perp AB$,$ND\perp AB$,点M,N在$\odot O$上.
(1)求证:$\overset{\frown}{AM}= \overset{\frown}{BN}$.
(2)若C,D分别为OA,OB的中点,则$\overset{\frown}{AM}= \overset{\frown}{MN}= \overset{\frown}{NB}$成立吗? 请说明理由.

答案： 【解析】：本题可根据圆的性质以及全等三角形的判定和性质来证明弧相等。
（1）求证：$\overset{\frown}{AM}= \overset{\frown}{BN}$
步骤一：连接$OM$、$ON$
因为$MC\perp AB$，$ND\perp AB$，所以$\angle MCO = \angle NDO = 90^{\circ}$。
步骤二：证明$OC = OD$
已知$AC = BD$，且$OA = OB$（同圆的半径相等），那么$OA - AC = OB - BD$，即$OC = OD$。
步骤三：证明$\triangle OCM\cong\triangle ODN$
在$\triangle OCM$和$\triangle ODN$中，$\begin{cases}OC = OD\\\angle MCO = \angle NDO = 90^{\circ}\\OM = ON\end{cases}$（同圆的半径相等），根据$HL$（斜边和一条直角边对应相等的两个直角三角形全等）可得$\triangle OCM\cong\triangle ODN$。
步骤四：证明$\angle MOC = \angle NOD$
由$\triangle OCM\cong\triangle ODN$，根据全等三角形的对应角相等，可得$\angle MOC = \angle NOD$。
步骤五：根据圆心角、弧的关系证明$\overset{\frown}{AM}= \overset{\frown}{BN}$
在同圆或等圆中，相等的圆心角所对的弧相等，因为$\angle MOC = \angle NOD$，所以$\overset{\frown}{AM}= \overset{\frown}{BN}$。
（2）判断$\overset{\frown}{AM}= \overset{\frown}{MN}= \overset{\frown}{NB}$是否成立并说明理由
步骤一：求出$\angle MOC$、$\angle MOD$、$\angle NOD$的度数关系
因为$C$，$D$分别为$OA$，$OB$的中点，所以$OC=\frac{1}{2}OA$，$OD=\frac{1}{2}OB$，又因为$OA = OB$，所以$OC = OD=\frac{1}{2}OM=\frac{1}{2}ON$（同圆半径相等）。
在$Rt\triangle OCM$中，$\cos\angle MOC = \frac{OC}{OM}=\frac{\frac{1}{2}OM}{OM}=\frac{1}{2}$，所以$\angle MOC = 60^{\circ}$。
同理，在$Rt\triangle ODN$中，$\angle NOD = 60^{\circ}$。
因为$\angle AOB = 180^{\circ}$，$AC = BD$，$C$，$D$分别为$OA$，$OB$的中点，所以$\angle MOD = 180^{\circ}- 60^{\circ}- 60^{\circ}= 60^{\circ}$。
步骤二：根据圆心角、弧的关系得出结论
在同圆或等圆中，相等的圆心角所对的弧相等，因为$\angle MOC = \angle MOD = \angle NOD = 60^{\circ}$，所以$\overset{\frown}{AM}= \overset{\frown}{MN}= \overset{\frown}{NB}$。
【答案】：（1）证明：连接$OM$、$ON$。
因为$MC\perp AB$，$ND\perp AB$，所以$\angle MCO = \angle NDO = 90^{\circ}$。
又因为$AC = BD$，$OA = OB$，所以$OC = OD$。
在$Rt\triangle OCM$和$Rt\triangle ODN$中，$\begin{cases}OC = OD\\OM = ON\end{cases}$，根据$HL$可得$\triangle OCM\cong\triangle ODN$，所以$\angle MOC = \angle NOD$。
在同圆或等圆中，相等的圆心角所对的弧相等，所以$\overset{\frown}{AM}= \overset{\frown}{BN}$。
（2）成立。理由如下：
因为$C$，$D$分别为$OA$，$OB$的中点，所以$OC = OD=\frac{1}{2}OM=\frac{1}{2}ON$。
在$Rt\triangle OCM$中，$\cos\angle MOC = \frac{OC}{OM}=\frac{1}{2}$，所以$\angle MOC = 60^{\circ}$，同理$\angle NOD = 60^{\circ}$，则$\angle MOD = 60^{\circ}$。
在同圆或等圆中，相等的圆心角所对的弧相等，所以$\overset{\frown}{AM}= \overset{\frown}{MN}= \overset{\frown}{NB}$。